MIKY & GENNY
IDENTITA' ED EQUAZIONI GONIOMETRICHE ---> INDICE
Identità goniometriche
Definizione - Si chiama identità goniometrica un'uguaglianza nella quale figurano funzioni goniometriche dello stesso angolo o di angoli dIversi, che risulta soddisfatta da qualsiasi valore attribuito ad essi.
Ad esempio, le relazioni
cos2α + sen2α = 1, tgα·ctgα = 1
Per verificare un'identità goniometrica, si procede allo stesso modo che per verificare le identità algebriche, cioè partendo da uno dei due membri, con successive trasformazioni, si cerca ottenere l'altro, oppure si trasformano contemporaneamente i due membri della stessa uguaglianza fino ad ottenere la stessa espressione.
Esempi
1)-Verificare l'identità:
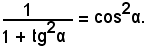
Partendo dal primo membro, si ottiene:
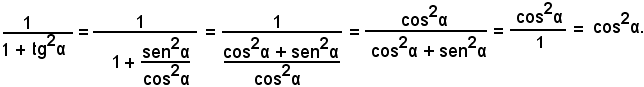
2)-Verificare l'identità:
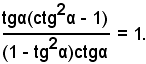
Partendo dal primo membro, ed esprimendo la cotangente in funzione della tangente, si ha:
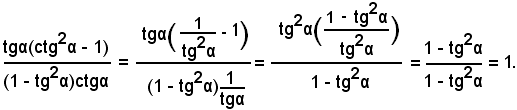
3)-Verificare l'identità:
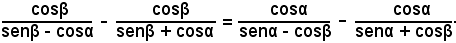
Definizione - Si chiama identità goniometrica un'uguaglianza nella quale figurano funzioni goniometriche dello stesso angolo o di angoli dIversi, che risulta soddisfatta da qualsiasi valore attribuito ad essi.
Ad esempio, le relazioni
cos2α + sen2α = 1, tgα·ctgα = 1
sono identità goniometriche.
Per verificare un'identità goniometrica, si procede allo stesso modo che per verificare le identità algebriche, cioè partendo da uno dei due membri, con successive trasformazioni, si cerca ottenere l'altro, oppure si trasformano contemporaneamente i due membri della stessa uguaglianza fino ad ottenere la stessa espressione.
Esempi
1)-Verificare l'identità:
Partendo dal primo membro, si ottiene:
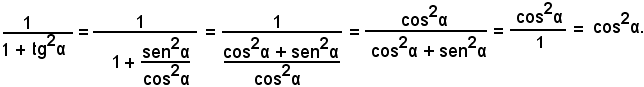
2)-Verificare l'identità:
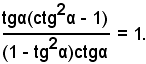
Partendo dal primo membro, ed esprimendo la cotangente in funzione della tangente, si ha:
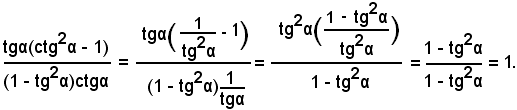
3)-Verificare l'identità:
Trasformando contemporaneamente i due membri, ed effettuando le operazioni indicate, segue:
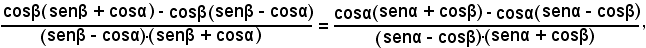
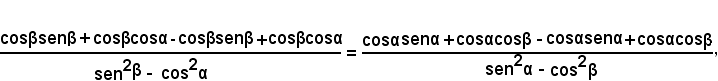
e semplificando si ha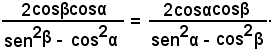
L'identità proposta risulta verificata, se si dimostra che:
sen2β - cos2α = sen2α - cos2β.
Trasportando in modo opportuno, si ha:
sen2β + cos2β = sen2α + cos2α,
che un virtù della relazione fondamentale, dà luogo all'identità numerica 1 = 1.
Equazioni goniometriche
Definizione - Si chiama equazione goniometrica un'uguaglianza nella quale le incognite sono gli angoli da cui dipendono una o più funzioni goniometriche.
Ad esempio, le relazioni:
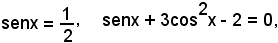
sono equazioni goniometriche nella sola incognita x.
Risolvere un'equazione goniometrica, significa trovare i valori degli angoli, o degli archi, incogniti per i quali l'equazione si trasforma in un'identità.
Esempio - Risolvere l'equazione senx = 1/2.
Evidentemente, essa è soddisfatta dal valore x = 30°, e anche dal valore x = 150°, in quanto angoli supplementari hanno lo stesso seno. Però, vi sono infiniti altri valori dell'angolo x che soddisfano l'equazione proposta, che si ottengono aggiungendo ai precedenti multipli qualsiasi di 360°, perchè come si è visto, la funzione seno è periodica di periodo 360°.
Si conclude quindi che tutte le soluzioni dell'equazione proposta sono date dalle formule:
x = 30° + 2k180°, x =150° + 2k180°,
dove k indica un numero intero qualsiasi, positivo, negativo o nullo.
Se si considerano le misure in radianti, le soluzioni dell'equazione proposta sono date da:
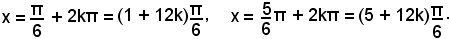
Prima di trattare in generale la risoluzione di un'equazione qualsiasi, è bene vedere come si risolvono alcune equazioni semplici ed importanti, dette equazioni elementari o tipiche. Ad esse si riporta poi la risoluzione di tutte le altre equazioni goniometriche.
Risoluzione dell'equazione
(1) senx = m,
con m numero dato.
Se m < -1, oppure m > +1, l'equazione è impossibile, perchè, come è noto, il seno assume soltanto valori comprese fra -1 e +1.
Se -1 ≤ m ≤ 1, considerato m positivo, si prenda sull'asse delle y un segmento OM, la cui misura rispetto al raggio del cerchio goniometrico sia m, e si conduca da M la parallela all'asse delle x. Si ottengono così due angoli
il cui seno è m.
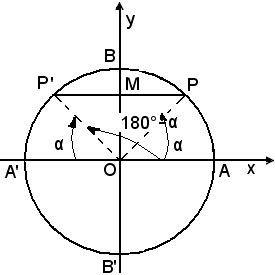
Allora, a causa della periodicità della funzione seno, la (1) è soddisfatta da ogni altro angolo, la cui misura differisca da α a 180° - α per un multiplo qualsiasi di 360°. La (1) ammette quindi infinite soluzioni x date dalle formule:
x = α + k360°, x = 180° - α + k360°,
cioè da
(2) x = α + 2k180°, x = -α + (2k + 1)180°.
Le (2) si possono raccogliere nell'unica formula
(3) x = (-1)hα + h·180°,
con h intero arbitrario, positivo, negativo o nullo.
Infatti, se h è pari, ponendo h = 2k, risulta (-1)h = +1 e si ha la prima delle (2); se invece h è dispari, ponendo h = 2k + 1, risulta (-1)h = (-1)2k + 1 = -1 e si ha la seconda delle (2); se h = 0, si ha la soluzione x = α e per h = 1 si ha l'altra x = 180° - α.
Si vuole ora risolvere l'equazione (1) nel caso in cui m sia negativo.
Posto x = 180° + y, dalla (1) segue:
senx = sen(180° + y)= -seny = m;
indicando allora con m' l'opposto di m, si ha l'equazione:
seny = m',
e siccome m' > 0, è del tipo già noto.
Allora, trovati i valori di y che la verificano, tutte le soluzioni dell'equazione proposta sono date quindi da x = 18° + y.
Quando si deve risolvere un'equazione goniometrica è preferibile esprimere le misure degli angoli in radianti; in tal caso tutte le soluzioni della (1) sono espresse dalla formula:
(3') x = (-1)hα + hπ,
essendo α la misura in radianti del minimo angolo positivo che verifica la stessa (1).
Si nota subito che dalla (2) risulta:
x - α = 2k·180°, x + α = (2k + 1)180°,
quindi
-gli angoli aventi lo stesso seno sono quelli la cui differenza è un multiplo pari dell'angolo piatto e quelli la cui somma è un multiplo dispari dell'angolo piatto.
Esempi
1)-Risolvere l'equazione:
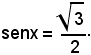
Essendo
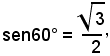
risulta α = 60°, e quindi tutte le soluzioni dell'equazione proposta sono date dalle formule:
x = 60° + 2k180°, x = 120° +2k180°,
o, introducendo le misure in radianti, dalle seguenti
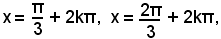
che possono raccogliersi rispettivamente nell'unica espressione
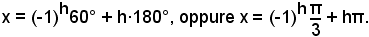
2)-Risolvere l'equazione:
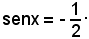
Essendo
l'equazione è soddisfatta da α = 30° + 180° ed ammette quindi tutte le soluzioni:
x = 30° + (2k + 1)180° , x = -30 + 2k·180°,
o, introducendo le misure in radianti, dalle seguenti
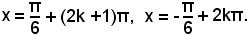
Risoluzione dell'equazione
sen2x = m2, con 0 ≤ m ≤ 1.
Estraendo la radice quadrata da ambo i membri dell'equazione, si ottiene:
senx = ± m,
quindi l'equazione proposta dà luogo alle seguenti equazioni
senx = m, senx = -m,
equivalenti ad essa.
Queste due equazioni si risolvono nel modo visto in precedenza.
Esempio - Risolvere l'equazione:
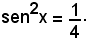
Estraendo la radice quadrata da ambo i membri dell'equazione, si ottiene:
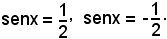
Essendo sen30° = 1/2, α = 30° e quindi tutte le soluzioni delle due equazioni sono date da:
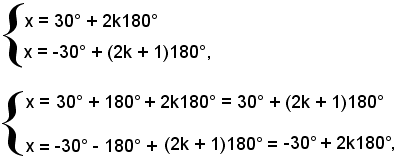
quindi
x = ± 30° + h180°,
oppure
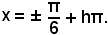
Risoluzione dell'equazione
(4) cosx = n,
con n numero dato.
Se n < -1, oppure n > 1, l'equazione è impossibile, perchè come è noto, il coseno assume valori compresi fra -1 e +1.
Se -1 ≤ n ≤ +1, considerato n positivo, si prenda sull'asse delle x, con verso positivo, un segmento OM, la cui misura rispetto al raggio del cerchio goniometrico sia n, e si conduca da M la parallela all'asse delle y. Si ottengono così due angoli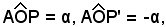
il cui coseno è n.
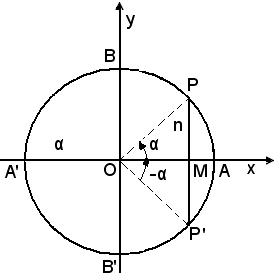
Allora, a causa della periodicità della funzione coseno, ogni angolo che differisca da α secondo multipli di 360° oppure da - α, risolve l'equazione proposta; tutte le sue soluzioni sono pertanto date dalle formule:
x = α + 2k180°, x = - α + 2k180°,
che si possono riunire nella formula
(5) x = 2k180° ± α,
o, introducendo le misure in radianti,
(5') x = 2kπ ± α.
Se poi n è negativo, con procedimento analogo a quello precedentemente visto, si trovano i due angoli opposti, uno con il secondo lato nel II quadrante e l'altro con il secondo lato nel III, che verificano la (4), quindi, tutte le soluzioni sono date dalla (5).
Dalla (5) risulta:
x - α = 2k180°, x + α = 2k180°,
quindi
-gli angoli aventi lo stesso coseno sono quelli la cui somma o la cui differenza è un multiplo dell'angolo giro.
Esempi:
1)-Risolvere l'equazione:
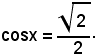
Essendo
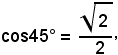
tutte le soluzioni sono date da
x = 45° + 2k180°, x = -45° + 2k180°,
ossia
x = ± 45° + 2k180°,
o in radianti
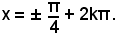
2)-Risolvere l'equazione:
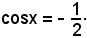
Essendo
x = 2k180° ± (180° - 60°) = (2k ± 1)180° ± 60°,
ossia
x = h180° ± 60°,
oppure
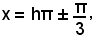
con h intero dispari, positivo, negativo o nullo.
Risoluzione dell'equazione
cos2x = n2, con 0 ≤ n ≤ 1.
Estraendo la radice quadrata da ambo i membri dell'equazione, si ottiene:
cosx = ± n,
quindi l'equazione proposta dà luogo alle seguenti equazioni
cosx = n, cosx = -n,
equivalenti ad essa.Queste due equazioni si risolvono nel modo visto in precedenza.
Risoluzione dell'equazione
6) tgx = p,
con p numero dato qualsiasi.
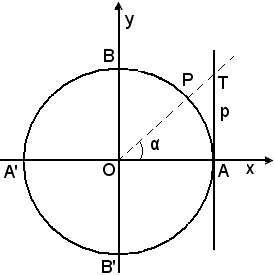
Supposto p positivo, si riporta sulla tangente in A alla circonferenza goniometrica, con verso positivo, il segmento AT di misura p rispetto al raggio. Congiungendo T con O si ottiene sulla circonferenza un punto P e l'angolo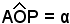
verifica la (6). Tenendo conto che la tangente è funzione
periodica di periodo 180°, risulta che tutte le soluzioni della
(6) sono date da:
(7) x = α + k180°,
oppure da
x = α + k π,
essendo k un numero intero qualsiasi.
Se invece p è negativo, ripetendo il procedimento illustrato in figura, si ottiene un angolo positivo α del II quadrante, che risolve la (6). Anche in tal caso tutte le soluzioni dell'equazione data sono espresse dalla (7).
Esempi
1)- Risolvere l'equazione:
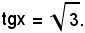
Essendo
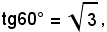
risulta α = 60° e quindi tutte le soluzioni dell'equazione sono espresse da
x = 60° + k180°,
oppure da
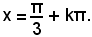
2)- Risolvere l'equazione:
tgx = -1.
Essendo tg45° = 1, risulta tg(180° - 45°) = -1, quindi tutte le soluzioni sono date da:
x = 180° - 45° +k180° = (k + 1)180° - 45°,
ossia
x = h180° - 45°,
oppure
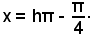
Risoluzione dell'equazione
tg2x = p2,
con p positivo.
Estraendo la radice quadrata da ambo i membri, si deducono le seguenti due equazioni:
tgx = p, tgx = -p
equivalenti all'equazione data. Ciascuna di esse si risolve col procedimento già visto.
Con procedimento del tutto analogo si risolvono le seguenti equazioni:
ctgx = p, secx = m, cosecx = m, con |m| ≥ 1;
ctg2x = p2, sec2x = m2, cosec2x = m2, con m ≥ 1.
Del resto tali equazioni si possono riportare alle seguenti:
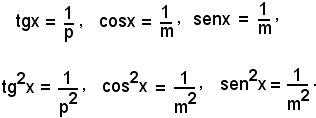
Dopo aver trattato la risoluzione delle equazioni tipiche, in sostanza equazioni binomie di primo e secondo grado in una data funzione goniometrica, ci si occupa ora in generale della risoluzione di altre equazioni, distinguendo due casi.
I caso: l'equazione contiene una sola funzione goniometrica
Se si indica la funzione goniometrica con una nuova incognita, si ottiene un'equazione algebrica che si può risolvere con i procedimenti trattati in algebra; poi si risolvono un certo numero di equazioni goniometriche tipiche.
Esempi
1)-Risolvere l'equazione:
2sen2x - 3senx + 1 = 0.
Ponendo senx = t, si ottiene l'equazione di secondo grado in t:
2t2 - 3t + 1 = 0,
le cui radici sono 1/2 e 1.
Si deducono quindi le due equazioni tipiche senx = 1/2 e senx = 1, la cui risoluzione è immediata.
La prima ammette le soluzioni
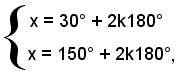
o anche
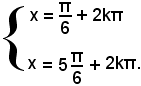
mentre la seconda
x = 90° + 2k180°,
o anche
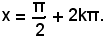
2)-Risolvere l'equazione:
8cos4x - 6cos2x + 1 = 0.
Ponendo cos2x = y, si ottiene l'equazione di secondo grado in y:
8y2 - 6y + 1 = 0,
le cui radici sono 1/2 e 1/4.
Si deducono quindi le due equazioni tipiche cos2x = 1/2 e cos2x = 1/4. Estraendo la radice quadrata da ambo i membri delle due equazioni, si hanno le quattro equazioni seguenti:
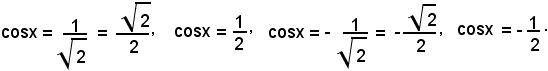
L'equazione
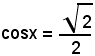
ammette le soluzioni
x = ±45° + 2k180°,
o anche
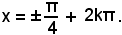
L'equazione
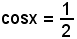
ammette le soluzioni
x = ±60° + 2k180°,
o anche
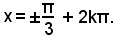
L'equazione
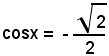
è soddisfatta da x = 180° - 45°, pertanto ammette le soluzioni
x = ±45° + (2k + 1)180°,
o anche
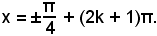
L'equazione
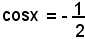
ammette le soluzioni
x = ±60° + (2k + 1)180°,
o anche
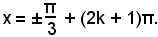
II caso: l'equazione contiene più di una funzione goniometrica
Per risolvere queste equazioni con l'impiego delle formule viste, si cerca di esprimere tutte le varie funzioni mediante una sola di esse e poi si procede come nel primo caso.
Esempi
1)-Risolvere l'equazione:
cos2x + 3senx = 3.
Esprimendo il coseno in funzione del seno mediante la formula cos2x = 1 - sen2x, l'equazione si trasforma in
1 - sen2x + 3sex = 3,
o anche, ordinando e semplificando, in
sen2x - 3sex + 2 = 0.
Ponendo senx = y, si ha l'equazione di secondo grado
t2 - 3t + 2 = 0,
le cui radici sono 1 e 2.
Si hanno quindi le due equazioni tipiche:
senx = 1, senx = 2.
La prima equazione ammette la soluzione
x = 90° + 2k180°,
o anche
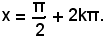
La seconda di tali equazioni è impossibile, perchè, come è noto, la funzione seno, in valore assoluto è sempre minore o uguale ad uno.
2)-Risolvere l'equazione:
(8) senx + cosx = a.
Si esprime la funzione coseno in funzione del seno mediante la formula
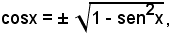
e si ottiene l'equazione irrazionale
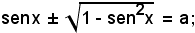
isolando il radicale, risulta
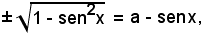
da cui, elevando al quadrato ambo i membri, risulta
1 - sen2x = a2 - 2asenx + sen2x,
e quindi, trasportando e ordinando,
2sen2x - 2asenx + (a2 - 1) = 0.
Ponendo senx = y, si ha l'equazione di secondo grado
2y2 - 2ay + (a2 - 1) = 0.
e si ottiene
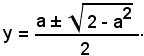
Affinchè quest'quazione ammetta radici reali, occorre che risulti
2 - a2 ≥ 0, o anche, estraendo la radice quadrata, sia
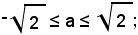
supposto ciò, si hanno le due equazioni tipiche:
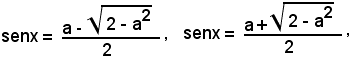
entrambe possibili, perchè si verifica facilmente che i valori
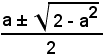
risultano minori di 1 in valore assoluto.
Sostituendo tale valore nell'equazione (8), si ha:
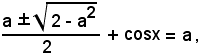
da cui si ricava
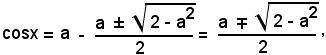
e quindi
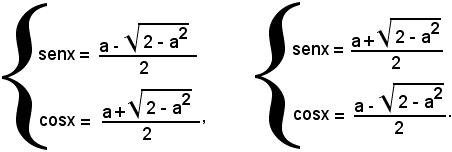
Si suppone ora a = 1, allora l'equazione
cosx + senx = 1
dà luogo ai due casi
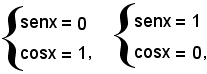
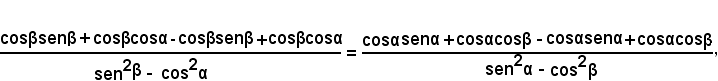
e semplificando si ha
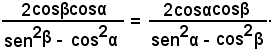
L'identità proposta risulta verificata, se si dimostra che:
Trasportando in modo opportuno, si ha:
che un virtù della relazione fondamentale, dà luogo all'identità numerica 1 = 1.
Equazioni goniometriche
Definizione - Si chiama equazione goniometrica un'uguaglianza nella quale le incognite sono gli angoli da cui dipendono una o più funzioni goniometriche.
Ad esempio, le relazioni:
sono equazioni goniometriche nella sola incognita x.
Risolvere un'equazione goniometrica, significa trovare i valori degli angoli, o degli archi, incogniti per i quali l'equazione si trasforma in un'identità.
Esempio - Risolvere l'equazione senx = 1/2.
Evidentemente, essa è soddisfatta dal valore x = 30°, e anche dal valore x = 150°, in quanto angoli supplementari hanno lo stesso seno. Però, vi sono infiniti altri valori dell'angolo x che soddisfano l'equazione proposta, che si ottengono aggiungendo ai precedenti multipli qualsiasi di 360°, perchè come si è visto, la funzione seno è periodica di periodo 360°.
Si conclude quindi che tutte le soluzioni dell'equazione proposta sono date dalle formule:
x = 30° + 2k180°, x =150° + 2k180°,
dove k indica un numero intero qualsiasi, positivo, negativo o nullo.
Se si considerano le misure in radianti, le soluzioni dell'equazione proposta sono date da:
Prima di trattare in generale la risoluzione di un'equazione qualsiasi, è bene vedere come si risolvono alcune equazioni semplici ed importanti, dette equazioni elementari o tipiche. Ad esse si riporta poi la risoluzione di tutte le altre equazioni goniometriche.
Risoluzione dell'equazione
(1) senx = m,
con m numero dato.
Se m < -1, oppure m > +1, l'equazione è impossibile, perchè, come è noto, il seno assume soltanto valori comprese fra -1 e +1.
Se -1 ≤ m ≤ 1, considerato m positivo, si prenda sull'asse delle y un segmento OM, la cui misura rispetto al raggio del cerchio goniometrico sia m, e si conduca da M la parallela all'asse delle x. Si ottengono così due angoli
il cui seno è m.Allora, a causa della periodicità della funzione seno, la (1) è soddisfatta da ogni altro angolo, la cui misura differisca da α a 180° - α per un multiplo qualsiasi di 360°. La (1) ammette quindi infinite soluzioni x date dalle formule:
cioè da
Le (2) si possono raccogliere nell'unica formula
(3) x = (-1)hα + h·180°,
con h intero arbitrario, positivo, negativo o nullo.
Infatti, se h è pari, ponendo h = 2k, risulta (-1)h = +1 e si ha la prima delle (2); se invece h è dispari, ponendo h = 2k + 1, risulta (-1)h = (-1)2k + 1 = -1 e si ha la seconda delle (2); se h = 0, si ha la soluzione x = α e per h = 1 si ha l'altra x = 180° - α.
Si vuole ora risolvere l'equazione (1) nel caso in cui m sia negativo.
Posto x = 180° + y, dalla (1) segue:
indicando allora con m' l'opposto di m, si ha l'equazione:
seny = m',
e siccome m' > 0, è del tipo già noto.
Allora, trovati i valori di y che la verificano, tutte le soluzioni dell'equazione proposta sono date quindi da x = 18° + y.
Quando si deve risolvere un'equazione goniometrica è preferibile esprimere le misure degli angoli in radianti; in tal caso tutte le soluzioni della (1) sono espresse dalla formula:
(3') x = (-1)hα + hπ,
essendo α la misura in radianti del minimo angolo positivo che verifica la stessa (1).
Si nota subito che dalla (2) risulta:
x - α = 2k·180°, x + α = (2k + 1)180°,
quindi
-gli angoli aventi lo stesso seno sono quelli la cui differenza è un multiplo pari dell'angolo piatto e quelli la cui somma è un multiplo dispari dell'angolo piatto.
Esempi
1)-Risolvere l'equazione:
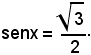
Essendo
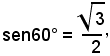
risulta α = 60°, e quindi tutte le soluzioni dell'equazione proposta sono date dalle formule:
o, introducendo le misure in radianti, dalle seguenti
che possono raccogliersi rispettivamente nell'unica espressione
2)-Risolvere l'equazione:
Essendo
l'equazione è soddisfatta da α = 30° + 180° ed ammette quindi tutte le soluzioni:
x = 30° + (2k + 1)180° , x = -30 + 2k·180°,
o, introducendo le misure in radianti, dalle seguenti
Risoluzione dell'equazione
sen2x = m2, con 0 ≤ m ≤ 1.
Estraendo la radice quadrata da ambo i membri dell'equazione, si ottiene:
senx = ± m,
quindi l'equazione proposta dà luogo alle seguenti equazioni
senx = m, senx = -m,
equivalenti ad essa.
Queste due equazioni si risolvono nel modo visto in precedenza.
Esempio - Risolvere l'equazione:
Estraendo la radice quadrata da ambo i membri dell'equazione, si ottiene:
Essendo sen30° = 1/2, α = 30° e quindi tutte le soluzioni delle due equazioni sono date da:
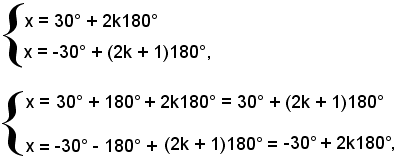
quindi
x = ± 30° + h180°,
oppure
Risoluzione dell'equazione
(4) cosx = n,
con n numero dato.
Se n < -1, oppure n > 1, l'equazione è impossibile, perchè come è noto, il coseno assume valori compresi fra -1 e +1.
Se -1 ≤ n ≤ +1, considerato n positivo, si prenda sull'asse delle x, con verso positivo, un segmento OM, la cui misura rispetto al raggio del cerchio goniometrico sia n, e si conduca da M la parallela all'asse delle y. Si ottengono così due angoli
il cui coseno è n.Allora, a causa della periodicità della funzione coseno, ogni angolo che differisca da α secondo multipli di 360° oppure da - α, risolve l'equazione proposta; tutte le sue soluzioni sono pertanto date dalle formule:
che si possono riunire nella formula
(5) x = 2k180° ± α,
o, introducendo le misure in radianti,
(5') x = 2kπ ± α.
Se poi n è negativo, con procedimento analogo a quello precedentemente visto, si trovano i due angoli opposti, uno con il secondo lato nel II quadrante e l'altro con il secondo lato nel III, che verificano la (4), quindi, tutte le soluzioni sono date dalla (5).
Dalla (5) risulta:
x - α = 2k180°, x + α = 2k180°,
quindi
-gli angoli aventi lo stesso coseno sono quelli la cui somma o la cui differenza è un multiplo dell'angolo giro.
Esempi:
1)-Risolvere l'equazione:
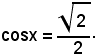
Essendo
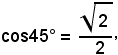
tutte le soluzioni sono date da
ossia
o in radianti
2)-Risolvere l'equazione:
Essendo
cos60° = 1/2, cos(180° - 60°) = -1/2
e quindi
x = 2k180° ± (180° - 60°) = (2k ± 1)180° ± 60°,
ossia
oppure
con h intero dispari, positivo, negativo o nullo.
Risoluzione dell'equazione
cos2x = n2, con 0 ≤ n ≤ 1.
Estraendo la radice quadrata da ambo i membri dell'equazione, si ottiene:
cosx = ± n,
quindi l'equazione proposta dà luogo alle seguenti equazioni
cosx = n, cosx = -n,
equivalenti ad essa.
Risoluzione dell'equazione
6) tgx = p,
con p numero dato qualsiasi.
Supposto p positivo, si riporta sulla tangente in A alla circonferenza goniometrica, con verso positivo, il segmento AT di misura p rispetto al raggio. Congiungendo T con O si ottiene sulla circonferenza un punto P e l'angolo
verifica la (6). Tenendo conto che la tangente è funzione
periodica di periodo 180°, risulta che tutte le soluzioni della
(6) sono date da:oppure da
x = α + k π,
essendo k un numero intero qualsiasi.
Se invece p è negativo, ripetendo il procedimento illustrato in figura, si ottiene un angolo positivo α del II quadrante, che risolve la (6). Anche in tal caso tutte le soluzioni dell'equazione data sono espresse dalla (7).
Esempi
1)- Risolvere l'equazione:
Essendo
risulta α = 60° e quindi tutte le soluzioni dell'equazione sono espresse da
x = 60° + k180°,
oppure da
2)- Risolvere l'equazione:
tgx = -1.
Essendo tg45° = 1, risulta tg(180° - 45°) = -1, quindi tutte le soluzioni sono date da:
ossia
oppure
Risoluzione dell'equazione
con p positivo.
Estraendo la radice quadrata da ambo i membri, si deducono le seguenti due equazioni:
tgx = p, tgx = -p
equivalenti all'equazione data. Ciascuna di esse si risolve col procedimento già visto.
Con procedimento del tutto analogo si risolvono le seguenti equazioni:
ctgx = p, secx = m, cosecx = m, con |m| ≥ 1;
ctg2x = p2, sec2x = m2, cosec2x = m2, con m ≥ 1.
Del resto tali equazioni si possono riportare alle seguenti:
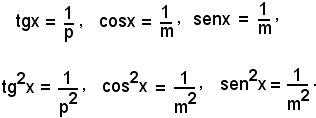
Dopo aver trattato la risoluzione delle equazioni tipiche, in sostanza equazioni binomie di primo e secondo grado in una data funzione goniometrica, ci si occupa ora in generale della risoluzione di altre equazioni, distinguendo due casi.
I caso: l'equazione contiene una sola funzione goniometrica
Se si indica la funzione goniometrica con una nuova incognita, si ottiene un'equazione algebrica che si può risolvere con i procedimenti trattati in algebra; poi si risolvono un certo numero di equazioni goniometriche tipiche.
Esempi
1)-Risolvere l'equazione:
2sen2x - 3senx + 1 = 0.
Ponendo senx = t, si ottiene l'equazione di secondo grado in t:
2t2 - 3t + 1 = 0,
le cui radici sono 1/2 e 1.
Si deducono quindi le due equazioni tipiche senx = 1/2 e senx = 1, la cui risoluzione è immediata.
La prima ammette le soluzioni
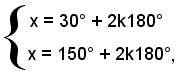
o anche
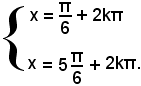
mentre la seconda
x = 90° + 2k180°,
o anche
2)-Risolvere l'equazione:
8cos4x - 6cos2x + 1 = 0.
Ponendo cos2x = y, si ottiene l'equazione di secondo grado in y:
8y2 - 6y + 1 = 0,
le cui radici sono 1/2 e 1/4.
Si deducono quindi le due equazioni tipiche cos2x = 1/2 e cos2x = 1/4. Estraendo la radice quadrata da ambo i membri delle due equazioni, si hanno le quattro equazioni seguenti:
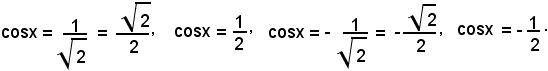
L'equazione
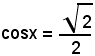
ammette le soluzioni
o anche
L'equazione
ammette le soluzioni
x = ±60° + 2k180°,
o anche
L'equazione
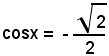
è soddisfatta da x = 180° - 45°, pertanto ammette le soluzioni
x = ±45° + (2k + 1)180°,
o anche
L'equazione
ammette le soluzioni
x = ±60° + (2k + 1)180°,
o anche
II caso: l'equazione contiene più di una funzione goniometrica
Per risolvere queste equazioni con l'impiego delle formule viste, si cerca di esprimere tutte le varie funzioni mediante una sola di esse e poi si procede come nel primo caso.
Esempi
1)-Risolvere l'equazione:
cos2x + 3senx = 3.
Esprimendo il coseno in funzione del seno mediante la formula cos2x = 1 - sen2x, l'equazione si trasforma in
1 - sen2x + 3sex = 3,
o anche, ordinando e semplificando, in
sen2x - 3sex + 2 = 0.
Ponendo senx = y, si ha l'equazione di secondo grado
t2 - 3t + 2 = 0,
le cui radici sono 1 e 2.
Si hanno quindi le due equazioni tipiche:
senx = 1, senx = 2.
La prima equazione ammette la soluzione
x = 90° + 2k180°,
o anche
La seconda di tali equazioni è impossibile, perchè, come è noto, la funzione seno, in valore assoluto è sempre minore o uguale ad uno.
2)-Risolvere l'equazione:
(8) senx + cosx = a.
Si esprime la funzione coseno in funzione del seno mediante la formula
e si ottiene l'equazione irrazionale
isolando il radicale, risulta
da cui, elevando al quadrato ambo i membri, risulta
e quindi, trasportando e ordinando,
2sen2x - 2asenx + (a2 - 1) = 0.
Ponendo senx = y, si ha l'equazione di secondo grado
2y2 - 2ay + (a2 - 1) = 0.
e si ottiene
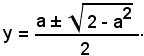
Affinchè quest'quazione ammetta radici reali, occorre che risulti
2 - a2 ≥ 0, o anche, estraendo la radice quadrata, sia
supposto ciò, si hanno le due equazioni tipiche:
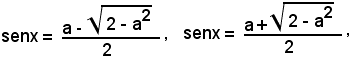
entrambe possibili, perchè si verifica facilmente che i valori
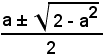
risultano minori di 1 in valore assoluto.
Sostituendo tale valore nell'equazione (8), si ha:
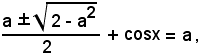
da cui si ricava
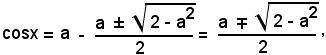
e quindi
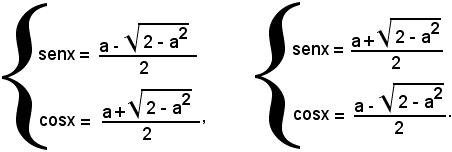
Si suppone ora a = 1, allora l'equazione
dà luogo ai due casi
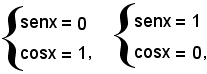
da cui rispettivamente risulta
x = 2k180°, x = 90° + 2k180°
o anche
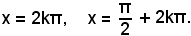
Se
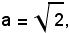
l'equazione
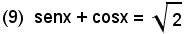
dà luogo all'unico caso
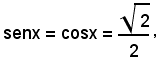
da cui
x = 45° + 2k180°,
o anche
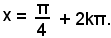
Nota bene
Si tenga ben presente il procedimento seguito per risolvere in questo caso la (8): prima si è eliminata una delle funzioni goniometriche e la si è trasformata in un'altra equazione contenente una sola funzione incognita. Dopo aver risolto quest'ultima equazione, si sono sostituiti i valori trovati nell'equazione (8), per determinare quelli corrispondenti dell'altra funzione e per avere i valori delle due funzioni incognite figuranti nella stessa (8).
Mediante tali valori è stato possibile individuare l'angolo, a meno di multipli di 360°, che soddisfa l'equazione data.
La determinazione dei multipli di tale angolo è necessaria e, allo scopo, si riesamina la (9).
Se si fosse considerato soltanto il valore
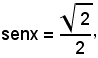
si sarebbe ottenuto
x = 45° + 2k180°, x = 135° + 2k180°,
mentre si verifica che i valori di x = 135° + 2k180° non soddisfano la (9).
Infatti, per x = 135° + 2k180° si ha:
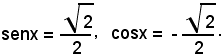
x = 2k180°, x = 90° + 2k180°
o anche
Se
l'equazione
dà luogo all'unico caso
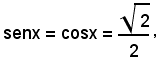
da cui
x = 45° + 2k180°,
o anche
Nota bene
Si tenga ben presente il procedimento seguito per risolvere in questo caso la (8): prima si è eliminata una delle funzioni goniometriche e la si è trasformata in un'altra equazione contenente una sola funzione incognita. Dopo aver risolto quest'ultima equazione, si sono sostituiti i valori trovati nell'equazione (8), per determinare quelli corrispondenti dell'altra funzione e per avere i valori delle due funzioni incognite figuranti nella stessa (8).
Mediante tali valori è stato possibile individuare l'angolo, a meno di multipli di 360°, che soddisfa l'equazione data.
La determinazione dei multipli di tale angolo è necessaria e, allo scopo, si riesamina la (9).
Se si fosse considerato soltanto il valore
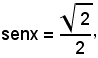
si sarebbe ottenuto
mentre si verifica che i valori di x = 135° + 2k180° non soddisfano la (9).
Infatti, per x = 135° + 2k180° si ha:
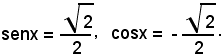
Segue:
sex + cosx = 0
e non l'equazione (9).
3)-Risolvere l'equazione:
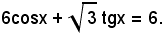
Si esprime la tangente in funzione del seno e del coseno mediante la formula
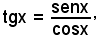
si ottiene l'equazione
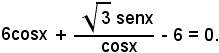
da cui, riducendo a forma intera, segue
Eliminando la funzione seno, si ottiene l'equazione irrazionale
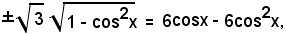
cioè
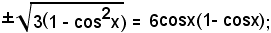
elevando al quadrato ambo i membri, si ha
3(1 - cos2x) = 36cos2x(1 - cosx)2,
cioè
(1 - cosx)(1 + cosx) - 12cos2x(1 - cosx)2 = 0,
e mettendo in evidenza 1 - cosx segue
(1 - cosx)[1 + cosx - 12cos2x(1 - cosx)],
o anche, sviluppando opportunamente,
(1 - cosx)(1 + cosx - 12cos2x + 12cos3x ) = 0.
Ricordando che un prodotto è uguale a zero, quando è uguale a zero almeno uno dei fattori, si possono scrivere le due equazioni:
1 - cosx = 0, 12cos3x - 12cos2x + cosx + 1 = 0.
La prima equazione dà cosx = 1, che sostituito nell'equazione data, risulta tg x= 0 e quindi si ha:
x = 2k180°.
Per risolvere la seconda equazione, si pone cosx = y e si ha la seguente equazione di terzo grado:
12y3 - 12y2 + y + 1 = 0,
che ammette la radice y = 1/2.
Applicando la regola di Ruffini, si ottiene la decomposizione:
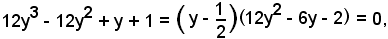
e quindi le radici
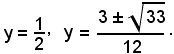
Essendo y = cosx, si hanno le tre equazioni tipiche:
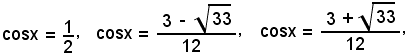
sostituendo poi questi valori nell'equazione proposta, si trova
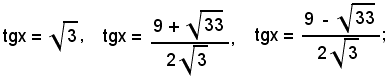e quindi
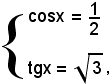
da cui
x = 60° + 2k180°.
Se non si fosse tenuto conto solo del valore cosx = 1/2, si sarebbero ottenuti anche gli altri valori x = -60° + 2k180° che non soddisfano l'equazione proposta.
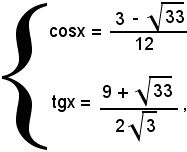
da cui
x = 180° - α1 + 2k180°,
dove α1 indica l'angolo del I quadrante, per cui
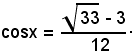
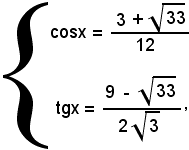
da cui
x = α1 + 2k180°,
dove α1 indica l'angolo del I quadrante per cui
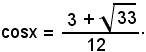
4)-Risolvere l'equazione:
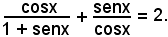
Riducendo a forma intera risulta:
cos2x + senx(1 + senx) = 2cosx(1 + senx),
e, sviluppando opportunamente,
cos2x + senx + sen2x = 2cosx(1 + senx).
Ricordando la relazione fondamentale
cos2x + sen2x = 1,
segue
1+ senx = 2cosx(1 + senx),
da cui, trasportando tutti i termini nel primo membro e mettendo in evidenza 1 + senx, si ha:
(1 + senx)(1 - 2cosx) = 0,
e quindi
1 + senx = 0, 1 - 2cosx = 0,
L'equazione 1 + senx dev'essere esclusa, perchè annullerebbe un denominatore dell'equazione proposta, quindi si considera solo l'equazione 1 - 2cosx = 0, cioè: cosx = 1/2, che ammette le soluzioni
x = ±60° + 2k180°,
o anche
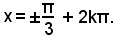
Sostituendo tale valore nell'equazione data, si ha:
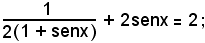
riducendo a forma intera e semplificando
4sen2x = 3,
cioè
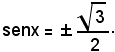
Tutti i valori precedentemente trovati, cioè
x = ±60° + 2k180°,
sono soluzioni accettabili per l'equazione data.
III caso - L'equazione è omogenea in seno e coseno
Ricordando dall'algebra la definizione di polinomio omogeneo in due variabili, le equazioni omogenee in seno e coseno sono della forma:
asenx + bcosx = 0, equazione di primo grado,
asen2x + bsenxcosx + ccos2x = 0, equazione di secondo grado,
e così via.
Esse si possono risolvere mediante il procedimento generale esposto in precedenza, ma conviene studiare un nuovo procedimento particolare, che permetta di ottenere la soluzione nel modo più rapido possibile.
Considerata un'equazione omogenea in seno e coseno di qualsiasi grado n, si dividono tutti i suoi termini per cosnx; si vede facilmente che la stessa equazione si trasforma in un'altra contenente solo la funzione tangente e si applica poi il procedimento del I caso.
Esempio - Risolvere l'equazione omogenea di terzo grado:
sen3x + sen2xcosx + 3senxcos2x - 3cos3x = 0.
Dividendo tutti i termini per cos3x, si ha:
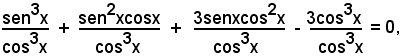
da cui, semplificando e ricordando che
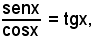
si ha l'equazione nella funzione tangente
tg3x + tg2x - 3tgx - 3 = 0.
Ponendo tgx = y, si ha:
y3 + y2 - 3y - 3 = 0,
che, mediante semplici trasformazioni, si può scrivere
y2(y + 1) - 3(y + 1)= 0,
cioè
sex + cosx = 0
e non l'equazione (9).
3)-Risolvere l'equazione:
Si esprime la tangente in funzione del seno e del coseno mediante la formula
si ottiene l'equazione
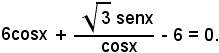
Eliminando la funzione seno, si ottiene l'equazione irrazionale
cioè
elevando al quadrato ambo i membri, si ha
3(1 - cos2x) = 36cos2x(1 - cosx)2,
cioè
e mettendo in evidenza 1 - cosx segue
(1 - cosx)[1 + cosx - 12cos2x(1 - cosx)],
o anche, sviluppando opportunamente,
(1 - cosx)(1 + cosx - 12cos2x + 12cos3x ) = 0.
Ricordando che un prodotto è uguale a zero, quando è uguale a zero almeno uno dei fattori, si possono scrivere le due equazioni:
La prima equazione dà cosx = 1, che sostituito nell'equazione data, risulta tg x= 0 e quindi si ha:
x = 2k180°.
Per risolvere la seconda equazione, si pone cosx = y e si ha la seguente equazione di terzo grado:
12y3 - 12y2 + y + 1 = 0,
che ammette la radice y = 1/2.
Applicando la regola di Ruffini, si ottiene la decomposizione:
e quindi le radici
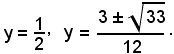
Essendo y = cosx, si hanno le tre equazioni tipiche:
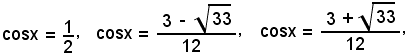
sostituendo poi questi valori nell'equazione proposta, si trova
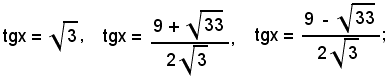
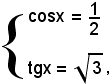
da cui
x = 60° + 2k180°.
Se non si fosse tenuto conto solo del valore cosx = 1/2, si sarebbero ottenuti anche gli altri valori x = -60° + 2k180° che non soddisfano l'equazione proposta.
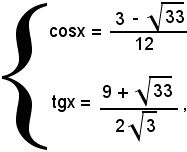
da cui
x = 180° - α1 + 2k180°,
dove α1 indica l'angolo del I quadrante, per cui
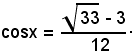
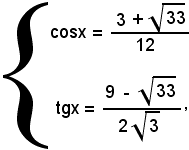
da cui
x = α1 + 2k180°,
dove α1 indica l'angolo del I quadrante per cui
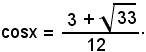
4)-Risolvere l'equazione:
Riducendo a forma intera risulta:
cos2x + senx(1 + senx) = 2cosx(1 + senx),
e, sviluppando opportunamente,
cos2x + senx + sen2x = 2cosx(1 + senx).
Ricordando la relazione fondamentale
cos2x + sen2x = 1,
segue
1+ senx = 2cosx(1 + senx),
da cui, trasportando tutti i termini nel primo membro e mettendo in evidenza 1 + senx, si ha:
(1 + senx)(1 - 2cosx) = 0,
e quindi
1 + senx = 0, 1 - 2cosx = 0,
L'equazione 1 + senx dev'essere esclusa, perchè annullerebbe un denominatore dell'equazione proposta, quindi si considera solo l'equazione 1 - 2cosx = 0, cioè: cosx = 1/2, che ammette le soluzioni
x = ±60° + 2k180°,
o anche
Sostituendo tale valore nell'equazione data, si ha:
riducendo a forma intera e semplificando
4sen2x = 3,
cioè
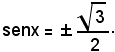
Tutti i valori precedentemente trovati, cioè
x = ±60° + 2k180°,
sono soluzioni accettabili per l'equazione data.
III caso - L'equazione è omogenea in seno e coseno
Ricordando dall'algebra la definizione di polinomio omogeneo in due variabili, le equazioni omogenee in seno e coseno sono della forma:
asenx + bcosx = 0, equazione di primo grado,
asen2x + bsenxcosx + ccos2x = 0, equazione di secondo grado,
e così via.
Esse si possono risolvere mediante il procedimento generale esposto in precedenza, ma conviene studiare un nuovo procedimento particolare, che permetta di ottenere la soluzione nel modo più rapido possibile.
Considerata un'equazione omogenea in seno e coseno di qualsiasi grado n, si dividono tutti i suoi termini per cosnx; si vede facilmente che la stessa equazione si trasforma in un'altra contenente solo la funzione tangente e si applica poi il procedimento del I caso.
Esempio - Risolvere l'equazione omogenea di terzo grado:
Dividendo tutti i termini per cos3x, si ha:
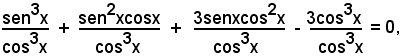
da cui, semplificando e ricordando che
si ha l'equazione nella funzione tangente
tg3x + tg2x - 3tgx - 3 = 0.
Ponendo tgx = y, si ha:
y3 + y2 - 3y - 3 = 0,
che, mediante semplici trasformazioni, si può scrivere
y2(y + 1) - 3(y + 1)= 0,
cioè
(y + 1)(y2 - 3)= 0,
Ricordando che y = tgx, si ha:
tgx + 1 = 0,
oppure
tg2 - 3 = 0.
Si deducono le seguenti tre equazioni:
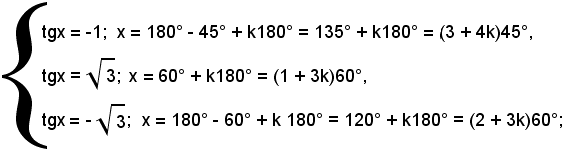
o anche, esprimendo le misure in radianti,
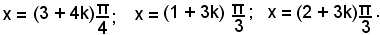
Si forniscono ora alcuni esempi di particolari equazioni goniometriche che, apparentemente complicate, si prestano ad una risoluzione rapida e inducono a riflettere sulle proprietà fondamentali delle funzioni goniometriche precedentemente trattate.
Esempio - Risolvere l'equazione:
sen(5x) = sen(3x).
Ricordando che gli angoli aventi lo stesso seno differiscono per un multiplo pari dell'angolo piatto oppure hanno per somma un multiplo dispari dell'angolo piatto, si ha:
5x - 3x = 2k180°, 5x + 3x = (2k + 1)180°,
da cui
2x = 2k180°, 8x = (2k + 1)180°,
e quindi
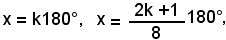
o anche, esprimendo le misure in radianti,
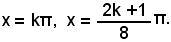
In generale si può considerare l'equazione
sen(mx) = sen(nx)
con m e n numeri reali qualsiasi.
Ripetendo il ragionamento precedente, si può scrivere
mx - nx = 2k180°, mx + nx = (2k + 1)180°,
e quindi
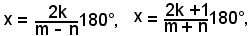
o anche, esprimendo le misure in radianti,
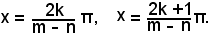
Analogamente si possono risolvere le equazioni del tipo:
cos(mx) = cos(nx).
Ricordando che gli angoli aventi lo stesso coseno sono quelli la cui somma o la cui differenza è un multiplo qualsiasi di 360°, si ha:
mx = nx + 2k180°, mx = -nx + 2k180°,
da cui
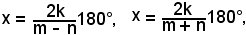
o anche, esprimendo le misure in radianti,
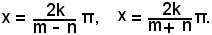
Con ragionamento del tutto analogo si possono risolvere le equazioni:
tg(mx) = tg(nx), cg(mx) = ctg(nx).
In entrambi i casi si ottiene:
mx = nx + k180°,
da cui
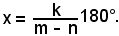
Si considera ora un altro tipo di equazione:
sen(mx) = cos(nx).
Ricordando che il coseno di un angolo è uguale al seno dell'angolo complementare, allora l'equazione si trasforma in:
sen(mx) = sen(90° - nx),
da cui, per quanto detto prima, si ha
mx = 90° - nx + 2k180°, mx = 180° - 90° + nx + 2k180°,
e quindi
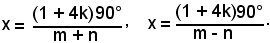
Analogamente si procede per l'equazione;
tg(mx) = ctg(nx),
che si trasforma in
tg(mx) = tg(90° - nx).
Ricordando che y = tgx, si ha:
oppure
tg2 - 3 = 0.
Si deducono le seguenti tre equazioni:
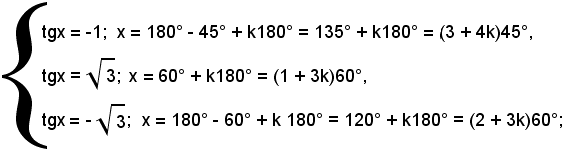
o anche, esprimendo le misure in radianti,
Si forniscono ora alcuni esempi di particolari equazioni goniometriche che, apparentemente complicate, si prestano ad una risoluzione rapida e inducono a riflettere sulle proprietà fondamentali delle funzioni goniometriche precedentemente trattate.
Esempio - Risolvere l'equazione:
sen(5x) = sen(3x).
Ricordando che gli angoli aventi lo stesso seno differiscono per un multiplo pari dell'angolo piatto oppure hanno per somma un multiplo dispari dell'angolo piatto, si ha:
5x - 3x = 2k180°, 5x + 3x = (2k + 1)180°,
da cui
e quindi
o anche, esprimendo le misure in radianti,
In generale si può considerare l'equazione
sen(mx) = sen(nx)
con m e n numeri reali qualsiasi.
Ripetendo il ragionamento precedente, si può scrivere
mx - nx = 2k180°, mx + nx = (2k + 1)180°,
e quindi
o anche, esprimendo le misure in radianti,
Analogamente si possono risolvere le equazioni del tipo:
cos(mx) = cos(nx).
Ricordando che gli angoli aventi lo stesso coseno sono quelli la cui somma o la cui differenza è un multiplo qualsiasi di 360°, si ha:
mx = nx + 2k180°, mx = -nx + 2k180°,
da cui
o anche, esprimendo le misure in radianti,
Con ragionamento del tutto analogo si possono risolvere le equazioni:
tg(mx) = tg(nx), cg(mx) = ctg(nx).
In entrambi i casi si ottiene:
mx = nx + k180°,
da cui
Si considera ora un altro tipo di equazione:
sen(mx) = cos(nx).
Ricordando che il coseno di un angolo è uguale al seno dell'angolo complementare, allora l'equazione si trasforma in:
sen(mx) = sen(90° - nx),
da cui, per quanto detto prima, si ha
mx = 90° - nx + 2k180°, mx = 180° - 90° + nx + 2k180°,
e quindi
Analogamente si procede per l'equazione;
che si trasforma in
tg(mx) = tg(90° - nx).