MIKY & GENNY
RAGGI DEI CERCHI INSCRITTI, CIRCOSCRITTI ED EX-INSCRITTI ---> INDICE
Raggio del cerchio inscritto in un triangolo
Si consideri il cerchio di centro O e raggio r inscritto in un triangolo qualsiasi ABC.Si rammenta che il centro del cerchio inscritto in un triangolo è il punto d'incontro delle bisettrici, chiamato incentro.
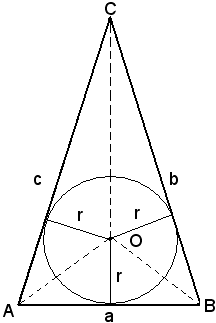
Congiungendo il centro O del cerchio con i tre vertici del triangolo si ottengono i tre triangoli OAB, OBC, OCA, ciascuno dei quali ha come base uno dei lati del triangolo dato, indicati con a, b, c, e per altezza il raggio r del cerchio inscritto. Le aree di ciascuno dei tre triangoli sono date rispettivamente da:
e quindi, se si indica con S l'area del triangolo ABC, si può scrivere
o anche, indicando con 2p il perimetro,
S = rp,
da cui
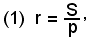
che è la formula cercata.
Raggio del cerchio circoscritto ad un triangolo
Si consideri il cerchio di centro O e raggio R circoscritto ad un triangolo qualsiasi ABC.Si rammenta che il centro del cerchio circoscritto ad un triangolo è il punto d'incontro degli assi dei lati, chiamato circocentro.
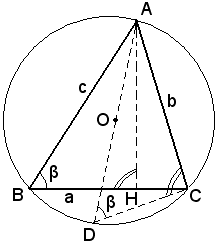
Si ha:
b = 2Rsenβ,
o anche, moltiplicando i due termini della frazione per ac,da cui
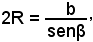
Essendo, come visto in precedenza,
ossia
2S = acsenβ,
allora, sostituendo questa espressione nel denominatore della (2), segue
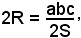
da cui
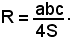
da cui
Raggi deI cerchi ex-inscritti ad un triangolo
E' noto dalla geometria che, per un qualsiasi triangolo oltre al cerchio inscritto, si possono considerare i cerchi ex-inscritti, cioè quei cerchi che sono tangenti alle rette individuate dai lati del triangolo, senza però che i punti di contatto risultino tutti e tre interni ai lati stessi.
I centri di tali cerchi, analogamente al centro del cerchio inscritto, si ottengono considerando le bisettrici degli angoli esterni del triangolo e quindi, evidentemente, esisteranno tre cerchi, ciascuno tangente ad un lato e ai prolungamenti degli altri due. I raggi di questi cerchi, tangenti internamente ai lati a, b, c, si indicano rispettivamente con ra, rb, rc.
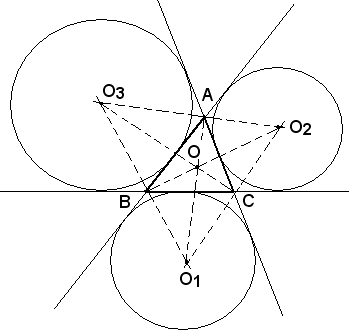
Dato il triangolo ABC, si consideri il cerchio ex-inscritto tangente internamente al lato a, avente per raggio ra, e sia O il suo centro. Congiungendo O1 con i vertici del triangolo ABC, si ottiengono i tre triangoli BCO1, ACO1, ABO1, i quali, rispetto alle basi BC, AC, AB hanno tutti per altezza il raggio ra; le loro aree sono perciò espresse rispettivamente da
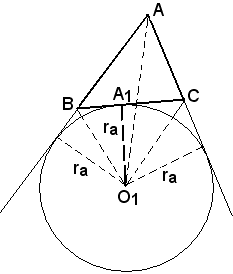
Inoltre l'area S del triangolo ABC è uguale alla somma delle aree dei due triangoli ACO1, ABO1, diminuita dell'area del triangolo BCO1, e quindi si può scrivere:
Ponendo
2p = a + b + c,
risulta
2p - 2a = a + b + c - 2a,
cioè
2(p - a) = b + c - a,
2(p - a) = b + c - a,
e sostituendo questa espressione nella formula precedente, si ha
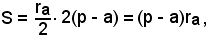
da cui
Per i raggi degli altri due triangoli ex-inscritti, analogamente si ha:
Tra il raggio del cerchio inscritto e quelli dei cerchi ex-inscritti, cioè tra
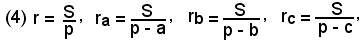
sussistono alcune relazioni interessanti.
Infatti, moltiplicando membro a membro le (4), risulta:
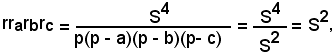
da cui
che è la prima delle formule cercate.
Invertendo le formule (4), si ha:
e sommando, risulta
o anche
e quindi
altra formula che si voleva stabilire.
Tra il raggio del cerchio inscritto e quelli dei cerchi ex-inscritti, sussistono altre relazioni usate meno delle precedenti. Infatti, se nella formula r = S/p si sostituisce ad S il valore eapresso dalla formula di Erone, si ha:
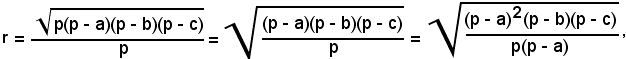
o anche
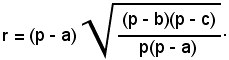
Ricordando la formula di Briggs relativa alla tangente, si ha:
Analogamente, risulta:
Se invece si sostituisce l'espressione di S, data dalla formula di Erone, nella formula
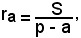
si ha:
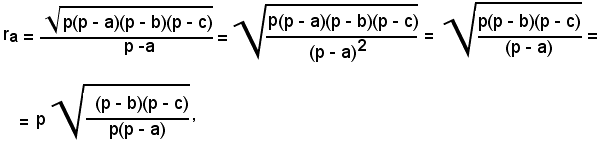
da cui, ancora per la formula di Briggs relativa alla tangente,
Analogamente, risulta: