PARTE I
**
Capitolo 1
FONDAMENTI
1. L'ANTINOMIA DI RUSSELL
"Sia w la classe di tutte quelle classi che non sono membri di se stesse.
Allora, qualunque sia la classe x, 'x è una w' è equivalente
a 'x non è una x'. Quindi, dando a x valore di w, 'w è una
w' è equivalente a 'w non è una w'."1
L'antinomia di Russell, per lettera comunicata a Frege il 16 giugno
del 1902, apre ufficialmente la crisi dei fondamenti della matematica2.
Essa origina dal principio di comprensione per il quale, data una condizione/proprietà
esiste l'insieme, o classe di tutti e soli gli oggetti che la soddisfano.
Presa la condizione: x Ï x, dove x sia una classe che non appartiene
a se stessa, si determina la corrispondente classe w di tutte le classi
che non appartengono a se stesse: w appartiene a se stessa? Posto che:
x Î w º x Ï x, sostituendo w a x si ottiene w Î w
º w Ï w.
In altre parole: se w appartiene a se stessa, allora soddisfa la condizione
definitoria della classe, che è di appartenere a se stessa; se w
non appartiene a se stessa, allora non soddisfa la condizione definitoria
della classe e perciò deve appartenere a se stessa.
Con il principio di comprensione Bertrand Russell faceva vacillare
in un colpo solo la teoria di Cantor, che su esso poggiava la costruzione
di insiemi, come estensioni di proprietà arbitrarie, e in modo più
diretto il progetto logicista di Frege. Mentre la rigorizzazione ottocentesca
dell'analisi prospettava a base elementare della matematica l'aritmetica,
Gottlob Frege intendeva ridurre ulteriormente l'aritmetica alla logica.
Le più semplici proposizioni aritmetiche, il concetto stesso di
numero naturale sarebbero emersi chiarificati nel loro fondamento logico.
Nei Grundlagen der Arithmetik del 1884 Frege definisce il numero
come la classe di tutte le classi equinumerose a una classe data, dove
due classi sono equinumerose, ovvero hanno la stessa potenza, se
e solo se gli elementi dell'una possono porsi in corrispondenza biunivoca
con gli elementi dell'altra. Così due sarà la classe di tutte
le classi a due membri. La definizione di numero, come la fornisce Frege,
sembra ancora a Russell "certamente definitiva e inattaccabile"3.
Il problema non sta qui; esso sorge dall'elevare a regola generale
per l'esistenza delle collezioni l'assioma di comprensione. Più
esattamente, rispetto al primo volume dei Grundgesetze der Arithmetik(1893),
l'antinomia di Russell colpisce il V dei principi lì postulati,
per il quale: V-a) se sotto due concetti cadono gli stessi oggetti, allora
i due concetti hanno estensioni uguali; V-b) se due concetti hanno estensioni
uguali, sotto di essi cadono gli stessi oggetti. Ma per stabilire che proprio
gli stessi oggetti cadano sotto le estensioni indicate, occorre avere già
determinato che cosa sia 'estensione di un concetto'. Tuttavia giungiamo
a contraddizione se assumiamo che per ogni concetto esista l'estensione
corrispondente.
Da un lato l'oggetto matematico due, in quanto classe di classi, non
si identifica con il concetto di due ma con la sua estensione. Ciò
consente a Frege di considerare gli enti matematici come oggetti dell'universo
logico. D'altro canto i concetti si identificano con funzioni, i cui valori
sono per qualunque argomento valori di verità. Nel primo volume
dei Grundgesetze risulta possibile stabilire una gerarchia delle funzioni,
quindi dei concetti, in gradi e tipi, in base alla natura e al numero degli
argomenti sostituiti alle variabili libere. Se in quest'idea di Frege Russell
ravvisava un'anticipazione della propria teoria dei tipi, si osserva che
si escludono dalla gerarchia gli oggetti. Anche se ciò ha particolari
ripercussioni, poiché il piano dell'estensione si situa a livello
oggettuale, l'antinomia di Russell si propone sia in termini di classi
(estensioni concettuali) che in termini di predicati (concetti). "Innanzi
tutto abbiamo l'enunciato in termini di predicati, che già venne
dato. Se x è un predicato, x può essere o non può
essere predicabile di se stesso. Ammettiamo che 'non predicabile di se
stesso' sia un predicato. Allora supporre che questo predicato sia, o non
sia, predicabile di se stesso, è autocontraddittorio. La conclusione,
in questo caso, sembra ovvia: 'la non predicabilità di se stessi'
non è un predicato. Enunciamo ora la stessa contraddizione in termini
di concetti-classe. Un concetto-classe può essere o non essere un
termine della sua propria estensione. La espressione 'concetto-classe che
non è un termine della sua estensione' è palesemente un concetto-classe.
Ma se esso è un termine della sua propria estensione, esso è
un concetto-classe che non è un termine della sua propria estensione,
e viceversa. Si deve pertanto concludere, contrariamente alle apparenze,
che 'concetto-classe che non è un termine della sua propria estensione'
non è un concetto-classe"4.
Il paradosso di Russell non era del resto l'unico. Di poco precedenti
si datano l'antinomia di Cesare Burali-Forti (1897) del massimo numero
ordinale e l'antinomia di Georg Cantor (1899) del massimo numero cardinale;
di poco successive l'antinomia di Jules Richard (1905) e quella di
Julius König (1905), per citare solo alcune tra le più note.
Ma più di ogni altra l'antinomia di Russell presentava come inderogabile
la necessità di una chiarificazione del concetto di insieme, chiamando
con esso in causa la possibilità di una fondazione logica dell'aritmetica.
2. IL SALVATAGGIO DEL PROGRAMMA LOGICISTA
2.a. La teoria dei tipi semplici
Malgrado Russell scopra l'antinomia durante la stesura di The Principles
of Mathematics (1903), l'ideale logicista continua a apparirgli perseguibile.
"La tesi fondamentale dell'opera, che la matematica e la logica siano identiche,
è una tesi che io non ebbi finora ragione di modificare"5.
Dei due scopi dell'opera il primo si enuncia in un programma affine
a quello di Frege: provare che i concetti e le proposizioni della matematica
pura sono riducibili a un numero piccolissimo di concetti e principi logici
fondamentali. Il compito si configura come prosecuzione dell'opera di Giuseppe
Peano, che derivava la teoria dei numeri naturali dalle tre idee fondamentali
di zero, numero e successore e da cinque postulati6. Poiché le tre
idee fondamentali si prestano a un numero infinito di interpretazioni,
ognuna delle quali soddisfa i cinque postulati, occorre superare quella
perfezione della aritmetizzazione. Persino quelle tre idee si possono spiegare
in termini di relazioni logiche tra classi. Ma il salvataggio del progetto
logicista richiede la soluzione dell'antinomia delle classi. Nell'appendice
B ai Principles, compare a tal fine un abbozzo della teoria dei tipi. A
essa spetta in primo luogo per ogni funzione proposizionale l'esame delle
condizioni alle quali ha significato. Essendo una funzione proposizionale
un'espressione con uno o più componenti indeterminati, finché
non si specifichi il campo di oggetti che la soddisfano, essa resta estranea
alla significanza.
"Ogni funzione proposizionale f(x), così si afferma, possiede,
oltre al suo sistema di valori (range) di verità, un sistema di
valori di significatività, ossia un sistema entro cui deve cadere
x se vogliamo che f(x) risulti comunque una proposizione, vera o falsa
che sia.7"
Considerando che le antinomie spesso nascondono una confusione tra
i livelli di espressione in gioco, esse si risolvono instaurando una distinzione
gerarchica tra i domini di significatività. "I sistemi di valori
di significatività formano dei tipi, ossia, se x appartiene al sistema
di valori di significatività di f(x) allora esiste tutta una classe
di oggetti (il tipo di x), i quali devono appartenere essi pure al sistema
di valori di significatività di f(x)"8. Ricordando come Frege
escludesse da ogni gerarchia l'oggettuale, che dà con l'estensione
al concetto insaturo il significato, si può già notare
per che via si ottenga una limitazione del principio di comprensione. Se
intendiamo la gerarchizzazione in modo tale che il tipo più basso
n consti di individui, alle funzioni che hanno individui come argomenti
attribuiamo il tipo n +1; alle funzioni che come argomenti hanno funzioni
di tipo n +1 il tipo n + 2 e così via. In tal modo non è
lecito dire che ogni condizione determini una classe, ma ogni condizione
sugli oggetti di un determinato tipo determina una classe al tipo successivo.
Le funzioni proposizionali che non rispettano la gerarchia sono in generale
prive di significato. Come tale si esclude l'antinomia di Russell, prevedendo
essa una relazione di appartenenza tra enti dello stesso tipo: x Î
x.
2.b. Il principio del circolo vizioso
La stratificazione in tipi semplici non rimedia a qualunque paradosso.
Nei Principia Mathematica l'esame delle principali contraddizioni che hanno
colpito la logica matematica rivela una caratteristica comune di riflessività
o autoriferimento. In ciascuna delle contraddizioni "si dice qualcosa su
tutti i casi di una qualche specie, e da quanto viene detto sembra generarsi
un nuovo caso il quale è e al contempo non è della stessa
specie dei casi che venivano presi in considerazione come tutti in ciò
che veniva detto"9.
Questo tratto caratterizza le totalità illegittime, tali per
cui, dato un insieme qualsiasi di oggetti, se supponiamo che abbia un totale,
esso dovrà contenere membri che presuppongono questo totale. La
totalità illegittima nasconde una definizione impredicativa, quella
cioè che definisce un ente attraverso la totalità o classe
cui appartiene, o quella che ricorre a termini, la cui definizione è
possibile soltanto facendo riferimento alla classe, cui l'ente da definirsi
appartiene. Dalle definizioni impredicative originano i circoli viziosi.
Riprendendo una suggestione di Henri Poincaré, Russell assume quel
principio del circolo vizioso che ci consente di evitare le totalità
illegittime. Esso appare così formulato: "Se - ammettendo che una
certa collezione abbia un totale - essa contenesse membri definibili soltanto
nei termini di quel totale, allora detta collezione non avrebbe un totale"10.
Oppure: "Qualunque cosa involga tutti i membri della collezione non deve
essere membro della collezione"11.
Nel contesto logicista il principio del circolo vizioso offre un'ossatura
alla gerarchia dei tipi, in quanto vale da criterio per fissare i limiti
della significatività rispetto alle funzioni proposizionali. Essendo
l'ambiguità una caratteristica precipua di una funzione, fino a
che non si assegni il valore della variabile, segue che f(x) ha un significato
definito solo se gli oggetti f(a), f(b), f(c), ecc. sono definiti. Perciò
"nessuna funzione può avere tra i propri valori qualcosa che presupponga
la funzione stessa"12.
Ma la gerarchia non è così semplice.
Se chiamiamo a-funzioni quelle significanti per un argomento dato a, constatiamo
che le varie a-funzioni non sono tutte di un tipo. Distinguiamo in particolare
quelle che non implicano riferimenti a nessun insieme di funzioni, le a-funzioni
predicative, da quelle che implicano il riferimento a una totalità
di funzioni. In questo caso il rimando a tutti o a alcuni dei valori che
una variabile può assumere, cioè la presenza di variabili
apparenti, richiama il rischio di nuove fallacie. "Ogniqualvolta, con frasi
intorno a 'tutti' o 'alcuni' valori che una variabile può sensatamente
assumere, diamo origine a un nuovo termine, questo nuovo termine non deve
essere uno dei valori che la variabile originaria può assumere,
dato che, se lo fosse, la totalità dei valori su cui la variabile
può estendersi sarebbe definibile soltanto in termini di se stessa
e ci troveremmo invischiati in un circolo vizioso"13.
Alla distinzione dei tipi si sovrappone quella degli ordini. Funzioni
proposizionali uguali per il tipo di argomento possono, a seconda delle
variabili apparenti che vi compaiono, appartenere a ordini diversi. Grazie
alla ramificazione in ordini, la variabile apparente universalmente quantificata,
tutti, non si riferisce più a tutti gli oggetti di un determinato
tipo ma viene circoscritta alla struttura tipo + ordine.
2.c. Assiomi controversi
La teoria dei Principia introduce alcuni problematici assiomi, la cui
necessità non è di ordine logico, ma risponde all'obiettivo
di ovviare a 'catastrofi matematiche'. Verrebbero a mancare la teoria del
transfinito e dei numeri reali, se non si assumesse l'assioma dell'infinito.
Esso equivale all'ipotesi che vi siano insiemi infiniti; enunciato come:
"Se n è un numero cardinale induttivo, vi è almeno una classe
di individui con n termini"14, l'assioma comporta quindi che il numero totale
degli individui al mondo non sia un numero induttivo (cioè un numero
naturale definito, mediante il processo di induzione matematica, come "posterità"
di 0 rispetto alla relazione di ogni numero con il suo successore). Infatti,
se l'assioma è vero, non esisteranno due cardinali con lo stesso
successore: dati m e n due numeri cardinali induttivi distinti, avremo
m + 1 diverso da n + 1. In modo simile potremmo affermare che n è effettivamente
diverso da n + 1, mentre senza l'assioma resta l'eventualità che
n e n + 1 siano entrambi la classe nulla. "Supponete che vi siano esattamente
nove individui nel mondo. (...) Allora i numeri cardinali induttivi da
0 a 9 sarebbero tali quali li conosciamo, ma 10 (definito come 9 +1) sarebbe
la classe-nulla. (...) Lo stesso sarà per 9+2, o in generale per
9+n, a meno che n non sia zero.15"
Adoperando i numeri per contare, anziché individui, classi,
classi di classi e così via, potremmo comunque raggiungere un numero
cardinale induttivo dato. Ma perdendo la progressione effettiva, non potremmo
passare all'intera classe dei numeri cardinali induttivi. E poiché
il numero dei numeri induttivi non è induttivo, non potremmo uscire
dall'aritmetica dei numeri interi finiti. Più impervio l'assioma
di riducibilità, che scaturisce dal conciliare la doppia gerarchia
di ordini e tipi con il recupero di parti della matematica, quali ad esempio
la dimostrazione del teorema di Cantor, secondo cui il numero dei membri
di un insieme dato a è sempre minore del numero dei sottoinsiemi
di a. L'assioma di riducibilità afferma che per qualsiasi funzione
proposizionale esiste una funzione predicativa formalmente equivalente
ad essa16. Dove una funzione si definisce predicativa quando è dell'ordine
immediatamente successivo a quello del suo argomento. L'assioma di riducibilità
rende inoperante la distinzione in ordini; infatti "mediante questa assunzione,
l'ordine di una funzione non predicativa può essere abbassato di
uno"17. Ma individuando nell'ordine più basso per ogni tipo l'ordine
predicativo, è possibile al contempo ascrivere alle proprietà
la stessa equivalenza che si ravvisa tra le funzioni. In tal modo se Y
è l'equivalente predicativa di f e gode della proprietà f,
l'ordine determinato da f gode della proprietà f. In altre parole
esiste sempre un predicato equivalente a qualunque proprietà individuata
da una funzione non predicativa. L'assioma di riducibilità permette
quindi di sfuggire alla conclusione che due oggetti possano concordare
in tutti i loro predicati senza essere identici. Considerando infatti che,
se tutte le proprietà di secondo ordine di x competono a y, allora
tutti i predicati di x competono a y, poiché 'avere tutti i predicati
di x' è già una proprietà di secondo ordine, non si
può, senza l'assioma, argomentare al contrario che se tutti i predicati
di x competono a y, allora tutte le proprietà di secondo ordine
di x devono competere a y.
E' possibile, come commenta Russell, che con un'applicazione meno drastica
del principio del circolo vizioso divenga evitabile l'assioma di riducibilità.
Approfondendo questa intuizione, nel 1925 (The Foundations of Mathematics)
Frank Plumpton Ramsey asserisce che la teoria dei tipi sviluppata nei Principia
consterebbe in realtà di due parti distinte: A) la gerarchia semplice
dei tipi; B) la ramificazione in ordini, che rende indispensabile l'assioma
di riducibilità. Ognuna di queste due parti, impropriamente unificate
per deduzione comune dal principio del circolo vizioso, si dirige contro
un certo genere di antinomie, che così risultano, a loro volta,
ripartite in: A) antinomie propriamente matematiche (sintattiche); B) antinomie
epistemologiche (semantiche)18. Le contraddizioni del gruppo B - punto uno,
cinque, sei, sette dell'elenco dei Principia - oggi risolte mediante la
differenziazione tra linguaggio e metalinguaggio, contengono tutte, secondo
Ramsey, un elemento extra-logico, che scaturisce, più che dalla
matematica stessa, dalla riflessione sulla matematica e dall'introdursi,
con questa istanza di pensiero, di un riferimento al significato delle
parole. Tali fallacie non sarebbero perciò importanti per un sistema
di logica simbolica; ma con questa constatazione vien meno l'esigenza di
mantenere l'assioma di riducibilità, che occorreva ad affrontarle.
Le contraddizioni che, come quella Russell, appartengono al gruppo A si
annullano invece direttamente, grazie alla teoria dei tipi semplici, osservando
che una funzione proposizionale non può prendere se stessa come
argomento: l'affermazione che una classe appartiene a se stessa non
è dunque né vera né falsa, ma priva di senso. In tal
modo Ramsey scioglie il nodo forse più scabroso della costruzione
dei Principia, ma al prezzo di restringere l'orizzonte della logica, che
più non ha accesso alle nozioni intensionali coinvolte nei paradossi
epistemologici.
3. ZERMELO: ASSIOMATICA DELLA TEORIA DEGLI INSIEMI
Obiezioni a Russell vengono anche da Ernst Zermelo. Fautore dell'autonomia
della teoria degli insiemi, Zermelo ritiene che la sua fondazione non accada
nell'alveo della logica. Occorre invece, nel rispetto di una specificità
matematica, caratterizzare l'universo di Cantor con assiomi peculiari.
Richiamandosi ai Grundlagen der Geometrie di David Hilbert, nel 1908 (Untersuchungen über die Grundlagen der Mengenlehre, I) Zermelo fornisce la prima veste assiomatica della teoria degli insiemi19. Anche per Zermelo la questione
dei paradossi discende dal definire l'insieme come estensione di un concetto
arbitrario. Pensando alla formulazione assiomatica come a ciò che
dà e precisa le condizioni sull'esistenza delle collezioni, il principio
di comprensione, troppo ampio e vago, è sostituito dall'assioma
di isolamento (o separazione). Esso può essere così enunciato:
se p(x) è una funzione proposizionale definita per tutti gli elementi
di un insieme M, M possiede un sottoinsieme Mp che contiene tutti e soli
gli elementi x di M, i quali soddisfano la proprietà p. Tale assioma
impone dunque, alla più generica concezione di insieme come aggregato
di oggetti distinti del nostro pensiero, due restrizioni: in primo luogo,
nessun insieme può essere definito in modo indipendente, ma sempre
e soltanto per separazione come sottoinsieme di un insieme già dato.
Ciò esclude nozioni contraddittorie come quella di classe di tutte
le classi, poiché l'esistenza della classe totale non è evidentemente
pensabile come prodotto dell'isolamento entro una classe precostituita.
In secondo luogo, il criterio di separazione deve essere "ben definito",
mediante le leggi universalmente valide della logica, rispetto alle relazioni
fondamentali, della forma "a Î b", che sussistono tra gli individui
(elementi, insiemi) del dominio della teoria assiomatizzata. Svaniscono
perciò criteri come "definibile in un numero finito di parole",
e con essi l'antinomia di Richard.
Il principio di separazione realizza la volontà di evitare insiemi
troppo grandi. Tale soluzione ha, come noterà Kurt Gödel nel
1944, un preludio nel saggio di Russell del 1905 On some difficulties in
the theory of transfinite numbers and order types. Per affrontare le contraddizioni
qui si avanzano tre proposte: la teoria dello zig-zag, quella della limitazione
di grandezza, e la no-classes theory. Di esse la seconda richiede appunto
che una classe possa esistere solo se non è troppo grande20.
Ma Zermelo è il primo a postulare l'assioma dell'infinito e
l'assioma di scelta, di cui Russell nei Principia fornisce, con l'assioma
moltiplicativo, una versione equivalente21. Sia a una classe e x la classe di tutte le sottoclassi di a esclusa la classe nulla: esiste almeno un selettore di x (cioè è sempre possibile scegliere in x un
singolo elemento m, n, r ... da ognuna delle sottoclassi di a, e combinare gli elementi scelti in una nuova classe). Da qui discende il teorema del
buon ordinamento, per il quale ogni classe può essere ben ordinata.
4. DAVID HILBERT: Grundlagen der Geometrie
4.a. Assiomi come definizioni implicite
Nei Grundlagen der Geometrie (1899) Hilbert dà corpo a una nuova
concezione assiomatica della geometria euclidea. Non possedendo più
nell'evidenza il valore di incontrovertibile verità, i postulati
ora divengono definizioni implicite. Come tali assolvono al compito di
delimitare la comprensione delle nozioni primitive che vi compaiono; ma
questo in via del tutto relazionale. I cinque gruppi di assiomi, che Hilbert
pone alla base dell'universo tridimensionale, prestano cioè schemi
di relazioni per i tre tipi di oggetti fondamentali: punti (che costituiscono
gli elementi della geometria della retta), rette (che insieme ai punti
formano gli elementi della geometria piana), piani (che con punti e rette
sono gli elementi della geometria solida), la cui identità è
di per sé priva di contenuto22. "Un concetto può essere logicamente
definito solo attraverso le sue relazioni con altri concetti. Queste relazioni,
formulate in enunciati determinati, le chiamo assiomi e pervengo in tal
modo al risultato che gli assiomi (eventualmente con l'aggiunta delle denominazioni
per i concetti) sono le definizioni dei concetti."23
La teoria, così pura nei suoi rapporti, consente a che gli enti
primitivi possano essere sostituiti con qualunque altro sistema di elementi
che soddisfi gli assiomi. "Si comprende da sé che ogni teoria è
solo un telaio, uno schema di concetti unitamente alle loro mutue relazioni
necessarie, e che gli elementi fondamentali possono venire pensati in modo
arbitrario. Se con i miei punti voglio intendere un qualunque sistema di
enti, per esempio il sistema: amore, legge, spazzacamino..., allora basterà
che assuma tutti i miei assiomi come relazioni tra questi enti perché
le mie proposizioni, per esempio il teorema di Pitagora, valgano anche
per essi. In altre parole: ogni teoria può essere sempre applicata
a infiniti sistemi di elementi fondamentali."24
La definizione dei concetti per via relazionale ha un antecedente storico
in geometria proiettiva con il principio di dualità, formulato da
Joseph-Diez Gergonne negli Annales de Mathématiques pures et appliquées (1826). Notando che nell'algebra una medesima equazione è soddisfatta da radici diverse, Gergonne ravvisa come, in alcune proposizioni vere della
geometria proiettiva, lo scambio di particolari termini permetta di ricavare
ancora proposizioni vere. Così resta vero l'enunciato che si ottiene
sostituendo alle nozioni di 'punto', 'collineare' e 'interseca', le nozioni
di 'retta', 'concorrente' e 'unito a'. In generale la legge di dualità
del piano consente che, in una proposizione vera intorno a figure proiettive
piane, si possano permutare tra di loro, lasciando immota la parola piano,
le parole punto e retta. Ad es.: due punti distinti di un piano individuano
una retta; due rette distinte di un piano individuano un punto. Ancora,
ferma rimasta la parola retta, si scambino le parole punto e piano per
la dualità dello spazio: due punti distinti individuano una retta;
due piani distinti individuano una retta. Il sistema delle relazioni tra
i simboli vale quindi indipendentemente dall'interpretazione che si assegna
ai simboli. Negli assiomi come definizioni implicite, la comprensione di
uno dei loro termini emerge grazie all'intergioco tra gli altri, ma la
legittimità teorica viene a poggiare sulla non contraddittorietà
formale.
4.b. Una prova di coerenza relativa
Nei Grundlagen der Geometrie Hilbert scarica il problema della coerenza
della geometria euclidea su quello della coerenza dei numeri reali. Interpretando
i punti e le linee come coppie di numeri reali e equazioni lineari, egli
dimostra che gli assiomi individuati per la geometria euclidea sono simultaneamente
soddisfatti nella geometria analitica25. Si ottiene in tal modo una prova
di coerenza relativa alla coerenza del sistema scelto come modello. Il
problema così slitta di teoria in teoria. Lungi dall'assicurarsi
un risultato stabile, si proporrà di lì a poco l'esigenza
di una prova assoluta di non contraddittorietà per l'aritmetica.
Ma la prova di coerenza ha già il senso della fondazione, perché
essa rappresenta per Hilbert la garanzia di esistenza e verità degli
enti matematici. "Se assiomi arbitrariamente stabiliti non sono in contraddizione,
con tutte le loro conseguenze, allora essi sono veri, allora esistono gli
enti definiti per mezzo di quegli assiomi. Questo è per me il criterio
della verità e della esistenza."26
Al confronto con l'universo non euclideo, l'affermazione può
suonare scottante. La coerenza di questi nuovi sistemi di assiomi fornirebbe
altrettante descrizioni vere dello spazio. E' chiaro che provando l'indipendenza
degli assiomi l'uno dall'altro, sempre grazie al modello dell'analitica
cartesiana, si conforta la legittimità di una geometria non euclidea.
Il caso ovvio ma eclatante si trova nell'assioma delle parallele, la cui
indipendenza sigilla addirittura la convivenza delle creazioni non euclidee.
Ma non può non sorgere il quesito se e come un sistema di assiomi
sappia caratterizzare, in modo prettamente unico, un insieme di oggetti
e relazioni. Al proposito Hilbert introduce tra gli assiomi di continuità
(V gruppo), quello di completezza lineare. "Il sistema dei punti di una
retta con le sue relazioni di ordinamento e congruenza non è suscettibile
di un ampliamento per il quale rimangono inalterate le relazioni sussistenti
tra gli elementi precedenti come pure le proprietà fondamentali
di ordinamento lineare e congruenza che seguono dagli assiomi I-III ed
anche V1".27
Il postulato di continuità archimedeo28 basterebbe da solo
a correlare con coordinate cartesiane uno spazio S, in modo che a ogni
suo punto corrispondano numeri reali. Ma la reciproca, che a ogni gruppo
di valori reali corrisponda un punto di S, non è garantita; quindi
si può ampliare S.
Se si vuole però che la coerenza valga come condizione di esistenza,
non basta la soddisfacibilità semplice, occorre la categoricità
del sistema degli assiomi che definisce lo spazio, perciò che si
ottenga coincidenza tra i punti di S e i numeri reali. Ma con la non estensibilità
per una retta si segna proprio l'unicità della struttura-modello.
Dopo la pubblicazione dei Grundlagen der Geometrie si osservò che,
invece di questa condizione, si poteva assumere quella più debole
della decidibilità di ogni enunciato del linguaggio in base agli
assiomi, cioè della completezza sintattica del sistema. In ogni
caso, nell'aspettativa che coerenza e completezza si richiamino l'un l'altra,
diventa urgente la ricerca di una prova di non contraddittorietà
conclusiva.
5. FINITARIO/INFINITARIO
Poiché la coerenza della geometria è rimandata a quella
dell'analisi, e l'analisi è a sua volta riducibile all'aritmetica
elementare, resta da fondare quest'ultima. L'antinomia di Russell riporta
al vivo la questione, palesando l'impossibilità di avvalersi dei
concetti della teoria degli insiemi. C'è per altro una differenza
essenziale tra il problema della coerenza della geometria e quello dell'aritmetica,
che per l'aritmetica non sembri lecito il rinvio a altra disciplina fondamentale.
La via consueta, che consiste nel dimostrare la non contraddittorietà
mediante un modello, risulta inadeguata. Infatti per l'aritmetica elementare,
già in virtù della successione dei numeri naturali globalmente
presa, occorrerebbe un modello complesso almeno quanto l'aritmetica stessa
e a infiniti elementi. Non abbracciabile nella sua interezza, non si avrebbe
modo certo per appurare che tale modello sia immune da contraddizioni.
Hilbert richiede quindi una preliminare delucidazione del concetto
di infinito. Nonostante lo sviluppo della matematica ne riveli la fertilità,
esso è fortemente aporetico. Come attestano le antinomie, l'accettazione
di totalità infinite in atto porta a conseguenze non controllabili.
Occorre quindi, sull'esempio dell'analisi, che riduce a operazioni con
il finito le operazioni sugli infinitesimi, perseguire in generale nei
procedimenti matematici una consimile riduzione. Tutte le espressioni matematiche
si dividono per Hilbert in due classi: enunciati reali (finitari) e enunciati
ideali (infinitari). Gli enunciati reali, o proposizioni dotate di senso,
condensano il nucleo della matematica finitaria. Di correttezza subitanea
e palese, essi vertono su oggetti al di qua del dubbio "che esistono intuitivamente
come qualcosa di immediato, prima di ogni pensiero"29. A priori della
rappresentazione30, tali oggetti costituiscono il prerequisito di ogni ragionamento
logico. Padroneggiabili in ogni loro parte e nelle loro semplici, mutue
relazioni, si configurano come quei segni, la cui forma per noi si impone,
con universalità e sicurezza riconosciuta, ovunque e in ogni tempo.
Come oggetto iniziale della teoria dei numeri Hilbert presceglie la cifra
1; un processo di prosecuzione, l'aggiungere 1, definisce ogni altro numero,
in modo da conservarne la concretezza discreta: sempre infatti si può
dominare, in una cifra, le parti di cui si compone. Si introducono inoltre
alcuni segni per la comunicazione: i numeri usuali, per abbreviare determinate
cifre, come 2 al posto di 1+1; i segni > e < per esprimere relazioni
di grandezza tra cifre e i segni = e ¹ per coincidenza o diseguaglianza; lettere minuscole nerette, per indicare una qualunque cifra non fissata.
Tipi di enunciati reali sono quindi: 2 + 3 = 3 + 2 e a + b = b+ a, dove il secondo comunica l'identità dei segni numerici a + b e b + a.
In sintesi il ragionamento finitario si compie "in forma di Gedankenexperimente
su oggetti che sono supposti come concretamente presenti": i numeri31. Ogni
costrutto finitario si situa nei limiti di questa rappresentabilità
di principio degli oggetti e di una altrettanto basilare eseguibilità
dei processi.
Ma non si ricava così l'intera matematica: il procedimento contenutistico
si rivela insufficiente ogni volta che desideriamo produrre asserzioni
su infiniti numeri o funzioni. Già l'algebra oltrepassa tale soglia
contenutistica, trattando le espressioni letterali come costrutti autonomi
formali: in a + b = b + a, a e b rivestono il ruolo di vere e proprie variabili
numeriche. A un simile enunciato ideale, Hilbert riguarda come a un oggetto
per l'applicazione di regole che consentono di derivare singoli enunciati
finitari: da a + b = b +a per la regola di sostituzione si desume 2 + 3
= 3 + 2. Quindi "la matematica diviene un patrimonio di formule: in primo
luogo, formule cui corrispondono comunicazioni contenutistiche di enunciati
finitari, e in secondo luogo altre formule che non significano niente e
che sono i costrutti ideali della nostra teoria"32.
Gli enunciati ideali si reputano senza significato, in quanto versano
su oggetti astratti o totalità infinite; ma dell'infinito non si
trova realizzazione né in natura né nel fondamento del nostro
operare razionale: il suo concetto travalica l'esperienza.
Una più urgente ragione impone di adottare gli enunciati ideali.
Se gravitiamo nella ristretta area finitaria, i tradizionali rapporti logici
sfumano di fronte alla quantificazione.
Una proposizione esistenziale della forma 'esiste una cifra n con la
proprietà A(n)' si intende finitariamente come giudizio parziale,
o comunicazione incompleta di un enunciato meglio determinato. Per esempio
il teorema di Euclide, che il numero dei numeri primi si estenda oltre
qualsiasi limite, trova traduzione in: posto p, intero primo, tra p + 1
e p! + 1 esiste certamente un nuovo numero primo. 'Esiste' abbrevia qui
la più completa ma conclusa combinazione di enunciati singolari
mediante "o": " p + 1 Ú p + 2 Ú p + 3 ... Ú p! + 1".
Si salta invece nel transfinito con l'asserzione più debole: esiste
un numero primo > di p, ovvero " p + 1 Ú p + 2 Ú p + 3 ... Ú ... in infinitum".
Un giudizio universale 'per ogni cifra n vale la proprietà A(n)'
è dal canto suo interpretabile finitariamente solo come giudizio
ipotetico, la cui legge si verifica per ogni singolo caso presente.
Ciò però lo rende non suscettibile di una negazione,
che dovrebbe praticare un esame infinito di tutti i numeri. Ne segue che
non si applica l'alternativa secondo cui tale giudizio o è soddisfatto
per ogni cifra o è refutabile mediante un controesempio.
Ma la rinuncia al principio del terzo escluso si evita, aggiungendo
agli enunciati reali i costrutti ideali; il sistema che ne scaturisce mantiene
la validità delle leggi della logica aristotelica.
6. TEORIA DELLA DIMOSTRAZIONE
Ora si sovrappone la distinzione tra un linguaggio oggetto, quello della
teoria di cui si vuole dimostrare la coerenza, e un metalinguaggio, quello
della matematica finitaria, con cui si procede alla dimostrazione. Perché
ciò accada in modo effettivo, occorre evidenziare la struttura sintattica
della teoria. Riprendendo la concezione del metodo assiomatico sviluppata
nei Grundlagen der Geometrie, Hilbert avanza la necessità della
formalizzazione: non avendo gli enunciati ideali, dal punto di vista finitario,
alcun significato, su di essi le operazioni logiche non si applicano alla
stessa maniera contenutistica che sugli enunciati reali. Bisogna quindi
riprodurre tali operazioni con il formalismo del calcolo logico: "in perfetta
analogia con il passaggio dalla teoria contenutistica dei numeri all'algebra
formale, noi consideriamo ora i segni e i simboli di operazioni sul calcolo
logico astraendo dal loro significato contenutistico"33. Quel carattere
di concretezza che i segni numerici rivestivano per la teoria dei numeri,
lo assumono adesso assiomi, formule, dimostrazioni per la metamatematica
o teoria della dimostrazione (Beweistheorie): "Nell'indagine che ora facciamo
è proprio la dimostrazione un qualcosa di concreto e di esibibile;
le argomentazioni contenutistiche si svolgono soltanto sulla dimostrazione"34.
La Beweistheorie consegue, nelle intenzioni di Hilbert, una vera e
propria critica della dimostrazione, allo scopo di rendere sicuri i teoremi
con cui il matematico opera. Questa sicurezza emerge dall'esibizione della
non contraddittorietà degli assiomi della teoria dei numeri, cosa
che si accerta in modo concreto se nessuna formula del tipo a ¹ a
è deducibile da essi. Si ottiene così, assieme all'auspicata
prova di coerenza assoluta per l'aritmetica, la giustificazione dell'aggiunta
degli elementi ideali. Hilbert ritiene che, per questa via, il problema
dei fondamenti verrebbe definitivamente eliminato e la matematica restituita
al rango di verità incontestabile.
7. COERENZA E ESISTENZA DEGLI OGGETTI MATEMATICI
Poiché "la proprietà richiesta dalla formula, cioè
quella di essere '1 ¹ 1', è una proprietà concretamente
constatabile della dimostrazione"35 con la ricerca della prova di coerenza
non si esorbita mai dall'ambito delle considerazioni intuitive.
L'intuitività della metamatematica sollecita il confronto con
le posizioni di Luitzen Egbertus Jan Brouwer. Per Brouwer, padre dell'intuizionismo,
la fonte del pensiero matematico è l'intuizione, come capacità
di considerare distintamente precisi concetti e costruzioni. Gli oggetti
matematici non hanno un'esistenza indipendente dal pensiero, ma essi esistono
in tanto che, attualmente compresi, se ne può fornire un metodo
di costruzione o un esempio36. Il criterio della costruibilità cautela
dalle antinomie, che per lo più nascono dall'attribuzione di una
validità universale al principio logico del terzo escluso37. E' innegabile
il fascino esercitato da queste critiche su Hilbert: "La sfida più
sottile e più appassionata lanciata dall'intuizionismo è
quella contro la validità del terzium non datur"38. Hilbert tuttavia
ritiene il terzium non datur assolutamente non responsabile dei paradossi
della teoria degli insiemi. Se inoltre il concetto di infinito in atto
è per entrambi di per sé non coglibile dalla mente, costruendo
una teoria intuizionista degli insiemi Brouwer non attesta l'intuizionismo
come parte della matematica, ma come la sola matematica possibile. Non
si verifica quindi un'emendazione strumentale, che operando sulla scala
del finito progressivamente si approssimi al limite dell'infinito. Il criterio
del costruttivo dà il periplo del pensiero e della giustificabilità
di parti della matematica. La non contraddittorietà, lungi dall'essere
garanzia di esistenza, è annullata come problema perché l'oggetto
matematico esiste solo e esclusivamente in quanto costruito in un modo
specifico. La confusione tra atto della costruzione e linguaggio matematico,
che caratterizza per Brouwer il logicismo, sta sottesa anche alla ricerca
hilbertiana della prova di coerenza39. Il formalista invece non aggiudica
un contenuto specifico, dato dall'intuizione, alle singole teorie, e non
rifiuta di principio alcuna parte della matematica, purché se ne
provi la coerenza. Quindi il finitismo diventa, in un modo molto classico,
un mezzo per riguadagnare l'infinito nella matematica. "Muovendosi sul
terreno del finitario, si deve dunque garantire il libero uso e il pieno
dominio del transfinito."40
La coerenza dell'aritmetica, una volta acquisita, consentirà
di ricostruire l'edificio matematico, fino a raccogliere la teoria degli
insiemi, dove soprattutto l'infinito alberga. La distinzione tra infinito
attuale e infinito potenziale permette di individuare, nei metodi finitari,
come operare in modo ricorsivo, a ogni passo in una finitezza che si può
ampliare indefinitamente. La coloritura fondazionale traspare da tutto
ciò, se si rammenta come la coerenza scandisca con l'esistenza la
verità di un insieme di enti matematici. Così si comprende
l'aspettativa hilbertiana della completezza; essa riverbera dapprima nella
convinzione della risolubilità di ogni problema matematico, che
si dichiari "necessariamente passibile di una rigorosa sistemazione, o
riuscendo a dare la risposta alla questione posta oppure mostrando l'impossibilità
di una sua risoluzione e quindi la necessità dell'insuccesso di
ogni tentativo"41. E' questa convinzione quasi un assioma, forse una legge
profonda dell'intelletto umano, e un possente stimolo al progredire nella
ricerca. Ciò però non comporta che la teoria della dimostrazione
sappia additare un metodo unitario e generale per affrontare qualunque
problema; piuttosto che sempre dovrebbe individuarsi, mediante un numero
finito di inferenze logiche, una adeguata risoluzione.
Esplicitamente però Hilbert pone la questione della completezza
solo al congresso internazionale dei matematici, tenutosi a Bologna nel
1928. L'asserzione della completezza per la teoria dei numeri ha veste
sintattica: "se agli assiomi della teoria dei numeri viene aggiunta una
formula appartenente alla teoria dei numeri ma non dimostrabile, allora
dal sistema di assiomi esteso può essere derivata una contraddizione"42.
Poiché operiamo entro la teoria della dimostrazione, emerge il
parallelo problema della completezza semantica per le regole logiche, cioè
se da tali regole siano derivabili tutte le formule logicamente valide.
NOTE
1. Whitehead, A. N., Russell, B., Principia Mathematica, Cambridge University Press, Cambridge, 1910-1913, 2° ed. 1925-1927; trad. it. parziale Introduzione ai Principia Mathematica, a cura di P. Parrini, La Nuova Italia, Firenze, 1977; cit. da p. 122.
2. La lettera in questione è riprodotta in Frege, G., Wissenschaftlicher Briefwechsel, a cura di G. Gabriel, H. Hermes, F. Kambartel, C. Thiel, A. Veraart, Meiner, Hamburg, 1976; trad. it. parziale di A. M. Obwexer, ed. a cura di C. Mangione, Alle origini della nuova logica. Epistolario scientifico, Boringhieri, Torino, 1983; pp. 183-184.
3. Russell, B., Introduction to Mathematical Philosophy, Allen and Unwin, London, 1919; trad. it. di L. Pavolini, Introduzione alla filosofia matematica, Longanesi, Milano, 1947; cit. da ed. del 1962 p. 39.
4. Russell, B., The principles of Mathematics, Cambridge University Press, Cambridge, 1903; trad. it. a cura di L. Geymonat, I principi della matematica, Longanesi, Milano, 1951; cit. da ed. del 1963 p. 167.
5. Russell, B., ibidem, p. 13.
6. Poiché per Peano il concetto di numero è un termine primitivo, gli assiomi non hanno il compito di definirlo, ma di enunciarne le proprietà. In modo informale i postulati di Peano sono:
a) zero è un numero;
b) il successore di ogni numero è un numero;
c) due numeri non possono avere lo stesso successore;
d) zero non è il successore di alcun numero;
e) ogni proprietà che appartenga tanto a zero quanto al successore immediato di ogni numero che goda di quella proprietà, appartiene a tutti i numeri (principio di induzione matematica).
7. Russell, B., I principi della matematica, op. cit., p. 713.
8. Russell, B., ibidem, p. 713.
9. Whitehead, A. N., Russell, B., op. cit., p. 126.
10. Whitehead, A. N., Russell, B., ibidem, p. 84.
11. Whitehead, A. N., Russell, B., ibidem, p. 84.
12. Ibidem, p. 87. Secondo Kurt Gödel (Gödel, K., Russell’s Mathematical Logic, in Schlipp P. A.(a cura di), The Philosophy of Bertrand Russell, Library of living philosophers, vol. 5, Northwestern University, Evanston, 1944; trad. it. di C. Cellucci, La logica matematica di Russell, in Cellucci, C.(a cura di), La filosofia della matematica, Laterza, Bari, 1967, pp. 81-122) nei Principia Mathematica si riscontrerebbero in realtà tre differenti principi del circolo vizioso, formulati in termini di definibilità, di involgimento e di presupposizione. "La prima forma è di particolare interesse perché solo questa rende impossibili le definizioni impredicative." Ma per Gödel questa è anche la forma meno plausibile delle tre: "si può dimostrare che il formalismo della matematica classica non soddisfa il principio del circolo vizioso nella sua prima forma, giacché gli assiomi implicano l’esistenza di numeri reali definibili in tale formalismo solo facendo riferimento a tutti i numeri reali". Ma essendo la matematica classica ricostruibile in base ai Principia, se ne deduce che il sistema stesso dei Principia non soddisfa al principio del circolo vizioso. (cit. da pp. 92-93.) Va comunque ricordato che, per Gödel, il principio del circolo vizioso nella sua prima forma diviene necessario soltanto se si assume, rispetto agli oggetti della logica e della matematica, una concezione nominalista, quale è appunto quella condivisa da Bertrand Russell e Alfred North Whitehead nei Principia. Intendendo invece le classi come oggetti reali, esso perderebbe il suo ruolo centrale.
13. Russell, B., Introduzione alla filosofia matematica, op. cit., p. 300.
14. Russell, B., ibidem, p. 212. A p. 192 della traduzione italiana dei Principia, si dà la seguente enunciazione dell’assioma dell’infinito:
Infin ax.=:aÎNC induct.Éa.$!a
cioè se a è un numero cardinale induttivo qualsiasi, esiste almeno una classe che ha a termini. In realtà secondo Russell non disponiamo né di argomenti logici né di argomenti empirici per stabilire se l’assioma dell’infinito sia vero o falso. Dal punto di vista logico, il fatto che il concetto di infinito non sia autocontraddittorio, non lo rende infatti dimostrabile; dal punto di vista empirico invece, i nostri sensi non sono abbastanza acuti per cogliere se la struttura fisica (non matematica) dello spazio, del tempo e del movimento nello spazio e nel tempo abbia grana continua o discreta.
15. Russell, B., Introduzione alla filosofia matematica, op. cit., p. 214.
16. "L’assioma di riducibilità sta nell’assunzione che, data una funzione qualsiasi f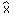
, vi è una funzione predicativa formalmente equivalente, ossia vi è una funzione predicativa che è vera quando fx è vera e falsa quando fx è falsa. In simboli l’assioma è
├ :($y):fx.ºx.y!x.". Russell fornisce poi l’assioma analogo per il caso di due variabili:
├:($y):f(x,y).ºx,y.y!(x,y) (Whitehead, A. N., Russell, B., op. cit., p. 115).
17. "L’assioma di riducibilità è equivalente all’assunzione che ‘qualsiasi combinazione o disgiunzione di predicati è equivalente ad un predicato singolo’, ossia all’assunzione secondo la quale, se asseriamo che x ha tutti i predicati che soddisfano una funzione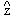 
))
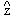18. Le antinomie semantiche elencate nei Principia sono quelle di: Epimenide (o del mentitore - nella sua forma più semplice, A afferma: “A mente”); Berry (o del più piccolo numero intero non nominabile in meno di n sillabe); König (o del più piccolo ordinale non definibile); Richard (per la sua descrizione si rimanda al cap. III della tesi). Figurano invece tra le antinomie sintattiche quelle di: Russell (già enunciata al § 1 cap. I); antinomia delle relazioni (variante dell’antinomia di Russell); Burali-Forti (se la serie bene-ordinata degli ordinali ha come numero ordinale W , la serie di tutti gli ordinali,W incluso, ha come ordinale W+1. Perciò W non è il numero ordinale di tutti gli ordinali).
19. Gli assiomi costitutivi per Ernst Zermelo (1908) sono: I) assioma di determinatezza (ogni insieme è determinato dai suoi elementi); II) assioma degli insiemi elementari (esiste un insieme - l’insieme vuoto - che non contiene alcun elemento; se a è un oggetto del dominio, esiste un insieme {a} il cui solo elemento è a; se a e b sono due oggetti del dominio, esiste un insieme {a, b}, i cui soli elementi sono a e b); III) assioma di isolamento (separazione); IV) assioma dell’insieme potenza (per ogni insieme x, si possono raccogliere in un insieme tutti i sottoinsiemi di x, compreso l’insieme vuoto e x medesimo); V) assioma dell’unione (per ogni insieme x, esiste un insieme x’ che contiene gli elementi dei suoi elementi); VI) assioma di scelta (per un insieme qualunque x di insiemi non vuoti, esiste un insieme che contiene un elemento di ogni elemento di x); VII) assioma dell’infinito (esiste un insieme infinito). Nel sistema presentato in "Über Grenzzahlen und Mengenbereiche", Fundamenta Mathematicae, vol. 16 (1930), pp. 29-47, si aggiungono: VIII) assioma di rimpiazzamento (se ad ogni elemento b di un insieme y si sostituiscono elementi arbitrari b’, l’unione di tutti i b’ costituisce un insieme); IX) assioma della fondazione (ogni insieme non vuoto ha un elemento minimale - Urelemente). (trad. it. "Numeri di confine e domini di insieme", in Cellucci, C. (a cura di), Il paradiso di Cantor, Bibliopolis, Napoli, 1978, pp. 177-195.)
20. Gödel, K., La filosofia di Bertrand Russell, op. cit. Mentre per la teoria della limitazione di grandezza, l’esistenza di una classe sarebbe quindi determinata dall’estensione di una funzione proposizionale, secondo la teoria zig-zag essa dipenderebbe "dal suo contenuto o senso (richiedendo un certo tipo di semplicità che andrebbe formulato con precisione)". Cioè le funzioni proposizionali, che fossero oscure o troppo complicate, cesserebbero di definire una classe. Gödel osserva che anche per la teoria zig-zag "è stato costruito recentemente un sistema logico, che presenta alcune caratteristiche essenziali di questo schema, cioè il sistema di Quine" (cit. da p. 89-90). Dalla teoria senza-classi, che considera le classi come façon de parler, si svilupperebbe invece l’opera successiva di Russell. Nella Introduzione ai Principia Mathematica si legge infatti: "I simboli per la classi, al pari di quelli per le descrizioni, sono, nel nostro sistema, simboli incompleti: ne vengono definiti gli usi, ma non si assumme affatto che presi da soli essi significhino qualcosa" (op. cit., p. 144). Contrariamente al realismo platonico che domina nei Principles, le classi sono ora "mere comodità simboliche o linguistiche, e non degli oggetti genuini" (ibid., p. 144), o, come si leggerà nella Introduzione alla filosofia matematica, "i simboli che indicano le classi sono una mera comodità, ma non rappresentano oggetti detti ‘classi’" (op. cit., p. 288). Resta peraltro travagliato il rapporto tra teoria delle classi e assioma di riducibilità. Quest’ultimo trova una ragione d’essere nel costituirsi come assunzione più debole di quella dell’esistenza delle classi: "sia a causa delle contraddizioni, che richiedono un trattamento più complicato se si assumono le classi, sia per l’opportunità di far sempre l’assunzione minima necessaria alla dimostrazione dei nostri teoremi, preferiamo assumere l’assioma di riducibilità piuttosto che l’esistenza delle classi" (Introduzione ai Principia Mathematica,op. cit., pp.118-119). Consapevoli della scarsa evidenza dell’assioma di riducibilità, nella successiva edizione dei Principia, Russell e Whitehead affermano esplicitamente come la sua giustificazione, di natura pragmatica, lasci insoddisfatti. Il tentativo di limitarne la portata adottando la tesi estensionale di Wittgenstein, che "le funzioni di proposizioni sono sempre funzioni di verità, e che una funzione può ricorrere in una proposizione soltanto attraverso i suoi valori" (ibidem, p. 172), provoca d’altro lato una complicazione della teoria delle classi: "dobbiamo adesso distinguere classi di ordini differenti composte di membri del medesimo ordine" (ibidem, p.219). Un problema ulteriore risiede, ad avviso di Russell, a fianco della meno grave impossibilità di dimostrare, senza l’assioma, il teorema di Cantor, nella mancata derivazione della teoria dei numeri reali. Va osservato per altro che nella Introduzione alla filosofia matematica Russell, dopo una dichiarazione di agnosticismo rispetto alla reale esistenza delle classi, conserva il tanto discusso assioma, ribadendone la necessità pragmatica. Ma, in quanto forma generalizzata del principio di identità degli indiscernibili di Leibniz, esso risulta indubitabilmente vero nel mondo empirico e non logicamente necessario: "Ammettere questo assioma in un sistema logico è quindi un difetto, anche se l’assioma empiricamente è vero. È per questa ragione che la teoria delle classi non può essere considerata completa" (Introduzione alla filosofia matematica,op. cit., p. 306).
21. L’assioma moltiplicativo nei Principia è così definito:
Mult ax.=:.k Î Cls ex2 excl. Ék:($ m):a Î k. Éa. m Ç a Î 1
se k è una classe di classi mutuamente esclusive, nessuna delle quali sia nulla, vi è almeno una classe m formata da uno e un solo membro di k. (Introduzione ai Principia Mathematica, op. cit., p. 191.)
22. "Noi consideriamo punti, rette e piani in certe relazioni reciproche ed indichiamo queste relazioni con parole come ‘giacere’, ‘fra’, ‘ congruente’; la descrizione esatta e completa, ai fini matematici, di queste relazioni segue dagli assiomi della geometria." Tuttavia i cinque gruppi di assiomi esprimono ancora per Hilbert "certi fatti fondamentali omogenei della nostra intuizione" e sono così individuati: I) Assiomi di collegamento (che caratterizzano la relazione di appartenenza di punti, rette, piani nello spazio tridimensionale); II) assiomi di ordinamento (che definiscono il concetto ‘fra’); III) assiomi di congruenza (che definiscono il concetto di congruenza e quindi quello di movimento); IV) assioma delle parallele (euclideo); V) assiomi di continuità (archimedeo e di completezza lineare). (Hilbert, D., Grundlagen der Geometrie, Teubner, Leipzig, 1899; trad. it. di P. Canetta, Fondamenti della geometria, Feltrinelli, Milano, 1970, citazione da p. 3.)
23. David Hilbert a Gottlob Frege, 22.09.1900, in Frege, G., op.cit., p.64.
24. David Hilbert a Gottlob Frege, 29.12.1899, ibidem, p. 52.
25. "Ci sono, come si riconosce, infinite geometrie che soddisfano agli assiomi I-IV e V 1, mentre ce n’è una sola, cioè la geometria cartesiana, in cui è valido nello stesso tempo anche l’assioma di completezza V 2." (Hilbert, D. Fondamenti della geometria, op. cit., p.37.)
26. David Hilbert a Gottlob Frege, 22.12.1899, in Frege, G., op. cit., p. 51.
27. Hilbert, D., Fondamenti della geometria, op. cit., p. 31.
28. Il postulato di Archimede afferma che, dati due segmenti diseguali a < b, esiste sempre un terzo segmento n(a), multiplo di a, per il quale si ha: n(a) > b.
29. Hilbert, D., "Über das Unendliche", Mathematische Annalen, 95 (1926), pp. 161-190; trad. it. "Sull’infinito", in Hilbert, D., Ricerche sui fondamenti della matematica, antologia a cura di V. Abrusci, Bibliopolis, Napoli, 1978, pp.233-266, cit. da p. 243.
30. Il riferimento a Immanuel Kant è esplicito e ricorrente in Hilbert, che ritiene le proprie indagini sui fondamenti della matematica in sintonia con la ricerca delle condizioni a priori di conoscenza ed esperienza tentate dal filosofo di Königsberg. Si legga per esempio: "Per la costruzione della teoria dei numeri abbiamo bisogno di una certa impostazione intuitiva a priori. Con ciò, quindi, mantiene la sua importanza l’idea basilare più generale della gnoseologia kantiana" (Hilbert, D. "Naturerkennen und Logik", Naturwissenschaften, 18 (1930), pp. 959-963; trad. it. "Conoscenza della natura e logica", in Hilbert, D., Ricerche sui fondamenti della matematica, op. cit., pp. 301-311, cit. da p. 306). Delimitando l’ambito del finitario, Hilbert pensa di ottenere appunto quelle conoscenze contrassegnate dal tratto dell’universale e del necessario, del tutto indipendenti dall’ esperienza. Perciò rispetto alla matematica pura, la teoria dell’a priori "è sostanzialmente l’impostazione finitaria da me caratterizzata" (ibidem, p. 309).
31. Hilbert, D., Bernays, P., Grundlagen der Mathematik, Springer, Berlin, vol. I, 1934; trad. it. parziale in Hilbert, D., Ricerche sui fondamenti della matematica, op. cit., pp. 332-474, cit. da p. 366.
32. Hilbert, D., Sull'infinito, op. cit., p. 249.
33. Hilbert, D., ibidem, p. 250.
34. Hilbert, D., "Neubegründung der Mathematik. Erste Mitteilung", Abhandlungen aus dem mathematischen Seminar der Hamburgischen Universität, 1 (1922), pp. 157-177; trad. it. "Nuova fondazione della matematica" in D. Hilbert, Ricerche sui fondamenti della matematica, op. cit., pp. 189-213, cit. da p. 204.
35. Hilbert, D., Sull'infinito, op. cit., p. 253.
36. Nelle lezioni di Cambridge Luitzen Egbertus Jan Brouwer designa l’intuizione basilare della matematica con il nome di ‘duità’ (twoity). Al vissuto introspettivo, la nozione di ‘passaggio al successivo’ appare, rispetto alla successione potenzialmente infinita dei numeri naturali, "percezione di un moto temporale. Tale percezione può essere descritta come separazione di un momento di vita in due cose distinte(...)". La duità è però recepita "nella forma vuota del substrato comune a tutte le duità", cioè nell’interpretazione psicologica il passaggio al successivo diviene, spogliato delle qualità dei numeri differenziati, un susseguirsi di posti vuoti. (Brouwer’s Cambridge Lectures on Intuitionism (a cura di D. van Dalen), Cambridge University Press, Cambridge, 1981; trad. it. di S. Bernini, Lezioni sull’intuizionismo: Cambridge 1946-51, Boringhieri, Torino, 1983, cit. da p. 30.) Nella rivisitazione della dottrina kantiana delle forme dell’intuizione pura, Brouwer abbandona quindi l’apriorità dello spazio, per aderire più nettamente a quella del tempo. A causa dello sviluppo delle geometrie non euclidee, non ha più senso infatti chiedersi quale geometria sarebbe vera per lo spazio della nostra esperienza. Dall’intuizione della duità, che riunisce le parti in quanto le tiene separate dal tempo, sono creati, assieme a tutti i numeri finiti, il continuo e il discreto, cioè il continuo lineare (o intuizione del "fra", ciò che non è esauribile per inserzione di nuove unità). Si confronti per altro la Critica della ragion pura, dove si definisce il numero, schema puro della quantità, "una rappresentazione, che raccoglie la successiva addizione di uno a uno (omogenei)". Esso non è che "l’unità della sintesi del molteplice di un’intuizione omogenea in generale, per il fatto che io produco il tempo stesso nell’apprensione dell’intuizione". (Kant, I., Kritik der reinen Vernunft, Hartknoch, Riga, 1781, 2° ed. 1787; trad. it. di G. Colli, Critica della ragion pura, Adelphi, Milano, 1976 (2 voll.), cit. da p. 222 della rist. per concessione a RCS, Milano, 1998.)
37. "In tutta la matematica intuizionista vale la summenzionata non-contraddittorietà, peraltro quasi evidente, del principio semplice di giudicabilità o del principio semplice del terzo escluso, cioè del principio del terzo escluso enunciato per un’arbitraria singola asserzione, entro un preassegnato dominio di entità matematiche." (Brouwer, L. E. J., Lezioni sull’intuizionismo: Cambridge 1946-51, op. cit., p. 34) L’applicazione del principio del terzo escluso è per Brouwer legittima in un sistema matematico finito; non così per un sistema infinito: "dato che non vi sono verità matematiche al di fuori del pensiero umano" (ibidem, p. 31), e questo può abbracciare, con ogni atto di costruzione matematica, solo una quantità finita di oggetti, il principio completo della giudicabilità è privo di senso, se non contraddittorio.
38. Hilbert, D., "Die Grundlagen der Mathematik", Abhandlungen aus dem mathematischen Seminar der Hamburgischen Universität, 6 (1928), pp. 65-85; trad. it. "I fondamenti della matematica", in Hilbert, D., Ricerche sui fondamenti della matematica, op.cit., pp. 267-289, cit. da p. 283.
39. Secondo Brouwer la vecchia scuola formalista, che comprende il primo Hilbert e Russell, è caratterizzata dal metodo logico-linguistico, che priverebbe la logica e la matematica della loro fondamentale differenza di carattere e di ogni autonomia. Il secondo Hilbert, inaugurando la nuova scuola formalista, riconoscerebbe invece un’autonomia alla metamatematica, la quale però confonde la perfezione del linguaggio matematico con la perfezione della matematica stessa. Così la critica inaugurata dal formalismo agisce di fatto sul solo linguaggio, che accompagna l’attività mentale matematica. La contraddizione che Hilbert si propone di eliminare dagli assiomi, con l’aiuto degli operatori logici, non è che una figura linguistica, la cui assenza non garantisce automaticamente della correttezza di una teoria. Al contrario "la matematica intuizionista è un’attività essenzialmente alinguistica" (Brouwer, L. E. J., Lezioni sull’intuizionismo: Cambridge 1946-51, op. cit., p. 30). Il linguaggio &egrvae; soltanto una tecnica, per memorizzare e comunicare le costruzioni matematiche.
40. Hilbert, D., "Die logischen Grundlagen der Mathematik", Mathematische Annalen, 88 (1923), pp. 151-177; trad. it. "I fondamenti logici della matematica", in D. Hilbert, Ricerche sui fondamenti della matematica, op. cit., pp. 215-231, cit. da p. 220. All’infinito resta, secondo Hilbert, il ruolo di idea, intesa nell’accezione kantiana come "concetto della ragione che oltrepassa ogni esperienza e con cui il concreto viene integrato nel senso della totalità". (Hilbert, D., "Sull'infinito", op. cit., p. 266.) Ora infatti in Kant l’idea è definita "un concetto necessario della ragione, cui non può essere dato, nei sensi, alcun oggetto corrispondente" (Kant, I., op. cit., p. 385); essa è al tempo stesso un concetto della totalità delle condizioni, per un condizionato dato. La totalità assoluta della sintesi delle apparenze dà luogo ai "concetti del mondo", fondamento di una cosmologia razionale, dove la ragione si invischia in una serie di antinomie, due delle quali, le cosiddette antinomie matematiche, coinvolgono la nozione di infinito (infinitudine del mondo nel tempo e nello spazio, infinita divisibilità delle parti). Hilbert ritiene infine che la propria analisi dell’infinito dissolva queste antinomie kantiane: "per questa via vengono svuotate le antinomie kantiane sullo spazio e sulla possibilità della suddivisione all’infinito" (Hilbert, D., "Conoscenza della natura e logica", op. cit., p. 304); si può perciò, con fiducia, proseguire nel lavoro matematico, senza rinunciare ad alcuna sua parte.
41. Hilbert, D., "Mathematische Probleme", Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 1900, pp. 253-297; trad. it. parziale "Problemi matematici", in D. Hilbert, Ricerche sui fondamenti della matematica, op. cit., pp. 145-162, cit. da p. 153.
42. Hilbert, D., "Probleme der Grundlegung der Mathematik" in Atti del Congresso internazionale dei matematici, Bologna, 3-10 ottobre 1928, Zanichelli, Bologna, 1929, vol. I, pp. 135-141; trad. it. "Problemi della fondazione della matematica", in D. Hilbert, Ricerche sui fondamenti della matematica, op. cit., pp. 291-300, cit. da p. 298.