Corde di lunghezza massima
 
Date due circonferenze C' e C'' che si intersecano in D ed E condurre per uno qualsiasi dei loro punti di intersezione una corda MN, con M appartenente a C' e N appartenente a C'', in modo tale che MN abbia lunghezza massima.
Osserviamo che comunque si tracci la corda MN  tutti i triangoli MEN  sono simili in quanto gli angoli EMD e END sono costanti in quanto angoli alla circonferenza che insistono sull'arco DE rispettivamente delle circonferenza C' e C''.
Dato che tutti i triangoli MEN sono simili quando MN è massimo lo sono anche gli altri due lati del triangolo cioe' i segmenti ME ed NE. Ma ME ed NE assumono la loro massima lunghezza quando sono diametri delle circonferenza alle quali appartengono.
Questo accade quando MN  è parallelo alla retta passante per i centri delle delle circonferenze e gli angoli MDE  e  NDE  sono entrambi retti.

Questo problema è risolto in modo diverso in una pagina di questo sito dedicata alla ricerca del

triangolo equilatero massimo circoscritto ad un triangolo qualsiasi.
 

Tra tutti i triangoli di data base inscritti in una circonferenza l'isoscele ha perimetro massimo.
 
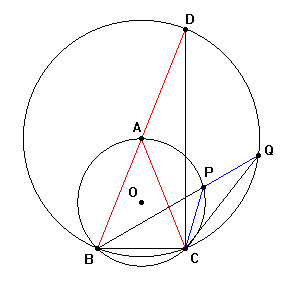
Data una circonferenza sia ABC il triangolo isoscele inscritto di base BC. Sul prolungamento di BA riportiamo il segmento AD = AC.

Il punto D appartiene ad una nuova circonferenza di centro A e diametro BD . L'angolo BAC è esterno al triangolo isoscele DAB  quindi l'angolo BAC = 2BDC perche' somma dei due interni non adiacenti.

Sulla prima circonferenza prendiamo un punto P diverso da A e prolunghiamo BP di un segmento PQ = PC. Gli angoli BAC e BPC sono uguali in quanto insistono sullo stesso arco BC inoltre l'angolo BPC è angolo esterno al triangolo isoscele QPC quindi BPC=2BQC e allora anche gli angoli BDC e BQC sono uguali quindi il punto Q appartiene alla stessa circonferenza alla quale appartiene il punto D.

Chiaramente la corda BQ = BP + PC raggiunge il suo massimo  quando coincide con il diametro della circonferenza cioè quando quando Q coincide con D e P coincide con A. In questo caso anche il perimetro del triangolo BPC raggiunge il massimo in quanto

 2p = BP+PC+CB .