Servois

Prenderemo in esame due problemi di allineamento che costituiscono una sorta di botta e risposta, avvenuto negli anni 1813-1814, tra due matematici francesi. I due personaggi hanno in comune la formazione e parte della loro carriera di ufficiali di artiglieria nell'esercito francese, rivoluzionario prima e napoleonico poi.

François Joseph Servois (1768 – 1847). Durante la Rivoluzione, nel 1793, entra nell’ esercito presso la scuola di artiglieria di Châlons-sur-Marne e nel 1794 è nominato tenente. Prosegue tutta la sua carriera di ufficiale come professore di matematica nelle scuole di artiglieria di Besançon, Châlons-sur-Marne e Metz fino al collocamento a riposo. Partecipò a diverse campagne militari senza interrompere la sua attività scientifica.

Joseph Diaz Gergonne (1771 – 1859). Nel 1791 entra come volontario nella Guardia Nazionale e nel 1792 partecipa alla battaglia di Valmy. Nel 1794 è tenente nelle scuola di artiglieria di Châlons-sur-Marne e nel 1795 è a Nimes dove ha sede il suo reparto e viene nominato professore di matematica trascendentale presso la locale École Centrale, successivamente sarà docente all’Università di Montpellier.

J-D Gergonne

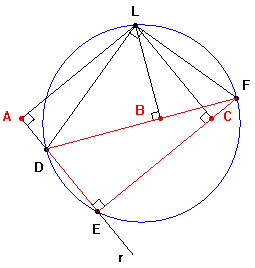
Servois propone un problema di "geometria pratica": prolungare una retta oltre un ostacolo che impedisce la visuale. In sostanza si tratta di individuare una costruzione che, dati due punti, consenta di determinare un terzo punto allineato con i precedenti senza prolungare il segmento dato.

Preso un punto L dal quale si possa vedere oltre l’ostacolo si traccia la retta LA e la retta r passante per A e perpendicolare a LA.

Si traccia la retta LB e per B la perpendicolare a LB che interseca la retta r in D.

Si traccia la retta LD e per L si manda la perpendicolare a LD e sia F l’intersezione della perpendicolare a LD con la retta BD

La perpendicolare a EF passante per L individua su EF il punto C allineato con A e B.

La costruzione è corretta e si basa sul teorema di Simson:
“Se da un punto qualsiasi di una circonferenza si mandano le perpendicolari ai lati di un triangolo inscritto i piedi delle perpendicolari sono allineati (retta di Simson)”. Robert Simson 1687-1768.

In effetti nella figura che si ottiene dalla costruzione si può osservare che il quadrilatero LDEF ha gli angoli opposti DLF e DEF entrambi retti dunque è inscrivibile in una circonferenza che ha per diametro DF quindi il triangolo DEF risulta inscritto e dal punto L si mandano le perpendicolari ai lati (o ai loro prolungamenti) quindi ...

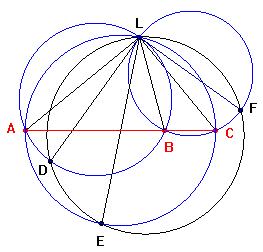Gergonne risponde con una costruzione del tutto equivalente a quella proposta da Servois. Per comodità manteniamo come riferimento la figura precedente, prendiamo la circonferenza alla quale appartiene il punto L e da L mandiamo le tre corde LD, LE, LF. Tracciamo le tre circonferenze che hanno per diametri le corde LD, LE, LF; le intersezioni a due a due delle tre circonferenze forniscono i punti A, B e C che risultano allineati. Noi ci limiteremo a mostrare l'equivalenza tra le due costruzioni.

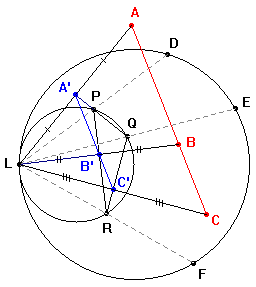Prendiamo un punto L su una circonferenza, per L mandiamo tre corde: LD, LE, LF. I punti medi di tali corde P, Q, R saranno i centri delle circonferenze che intersecandosi a due a due danno i punti A, B e C. E' noto che il luogo dei punti medi delle corde aventi in comune il punto L è una circonferenza tangente internamente in L alla circonferenza data e che ha come diametro il raggio della circonferenza assegnata.
Dato che i punti di intersezione di due circonferenze sono simmetrici rispetto alla retta passante per i centri tracciamo tali rette che formano il triangolo PQR. I punti A, B e C simmetrici di L rispetto a tali rette sono i punti di intersezione delle tre circonferenze prese a due a due.
La simmetria assiale presuppone la perpendicolarità dunque i segmenti LA, LB e LC sono ortogonali ai lati del triangolo PQR. Quindi se i piedi delle altezze A', B', C' sono allineati (Teorema di Simson) allora lo sono anche i punti A, B, C e viceversa in quanto i triangoli che hanno un vertice comune in L hanno i lati in proporzione, quindi sono simili, e allora AC // A'C'.