Risposta al gradino.

Sia:

$$x\left(t\right)=\left\{ \begin{array}{l} 0\qquad\forall t\in\Re:t\le0\\ A\qquad\forall t\in\Re:t\ge0\end{array}\right.$$

si ha:

$$a_{2}\frac{d^{2}y\left(t\right)}{dt^{2}}+a_{1}\frac{dy\left(t\right)}{dt}+a_{0}y\left(t\right)=b_{0}A$$

dividendo primo e secondo membro per $a_{0}\ne0$, si ha:

$$\frac{a_{2}}{a_{0}}\frac{d^{2}y\left(t\right)}{dt^{2}}+\frac{a_{1}}{a_{0}}\frac{dy\left(t\right)}{dt}+y\left(t\right)=\frac{b_{0}}{a_{0}}A$$

dove:

$$\frac{1}{\omega_{0}^{2}}=\frac{a_{2}}{a_{0}}$$

$\omega_{0}$ è la pulsazione naturale del sistema:

$$\frac{2\zeta}{\omega_{0}}=\frac{a_{1}}{a_{0}}$$

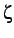$\zeta$ è lo smorzamento ed:

$$K=\frac{b_{0}}{a_{0}}$$

$$\frac{1}{\omega_{0}^{2}}\frac{d^{2}y\left(t\right)}{dt^{2}}+\frac{2\zeta}{\omega_{0}}\frac{dy\left(t\right)}{dt}+y\left(t\right)=KA$$

l'equazione caratteristica è dell'omogenea associata è:

$$\frac{1}{\omega_{0}^{2}}\alpha^{2}+\frac{2\zeta}{\omega_{0}}\alpha+1=0$$

che da' come soluzioni:

$$\alpha_{1,2}=\frac{-\frac{2\zeta}{\omega_{0}}\pm\sqrt{\left(\frac... ...ta}{\omega_{0}}\right)^{2}-\frac{4}{\omega_{0}^{2}}}}{\frac{2}{\omega_{0}^{2}}}$$

$$\alpha_{1,2}=\frac{-\frac{2\zeta}{\omega_{0}}\pm\frac{2}{\omega_{... ...}}{\frac{2}{\omega_{0}^{2}}}=\omega_{0}\left(-\zeta\pm\sqrt{\zeta^{2}-1}\right)$$

ovvero, ponendo:

$$\omega_{i}=\omega_{0}\sqrt{\zeta^{2}-1}\qquad\omega_{r}=\omega_{0}\zeta$$

si ha:

$$\alpha_{1,2}=-\omega_{r}\pm\omega_{i}$$

se è:

$$\zeta^{2}-1<0$$

si ha:

$$\alpha_{1,2}=\omega_{r}\pm j\omega_{i}$$

$$y\left(t\right)=\frac{KA}{2j\omega_{i}}\left(\omega_{r}-j\omega_{... ...\omega_{i}}\left(-\omega_{r}+j\omega_{i}\right)e^{-\omega_{r}t+j\omega_{i}t}+KA$$

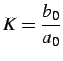
$$y\left(t\right)=KA\left[\frac{1}{2j\omega_{i}}\left(\omega_{r}-j\... ...a_{i}}\left(\omega_{r}-j\omega_{i}\right)e^{-\omega_{r}t+j\omega_{i}t}+1\right]$$

$$\frac{y\left(t\right)}{KA}=\frac{1}{2j\omega_{i}}\left(\omega_{r}... ...right)\left(e^{\omega_{r}t-j\omega_{i}t}-e^{-\omega_{r}t+j\omega_{i}t}\right)+1$$

se invece:

$$\zeta^{2}-1=0$$

si ha:

$$\alpha_{1,2}=\omega_{r}$$

$$y\left(t\right)=-KA\left(e^{-\omega_{0}t}-\omega_{0}te^{-\omega_{0}t}+1\right)$$

$$\frac{y\left(t\right)}{KA}=e^{-\omega_{0}t}\left(1-\omega_{0}t\right)+1$$

ed infine:

$$\zeta^{2}-1>0$$

$$\alpha_{1,2}=-\omega_{r}\pm\omega_{i}$$

$$y\left(t\right)=KA\left[\frac{1}{2\omega_{i}}\left(\omega_{r}-\om... ...ga_{i}}\left(\omega_{r}-\omega_{i}\right)e^{-\omega_{r}t+j\omega_{i}t}+1\right]$$

$$\frac{y\left(t\right)}{KA}=\frac{1}{2\omega_{i}}\left(\omega_{r}-... ...\right)\left(e^{\omega_{r}t-\omega_{i}t}-e^{-\omega_{r}t+j\omega_{i}t}\right)+1$$

Figure: Risposta al gradino per un sistema del secondo ordine.