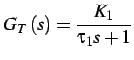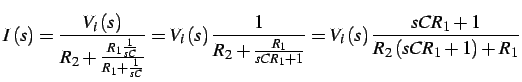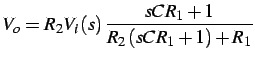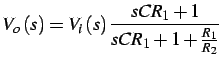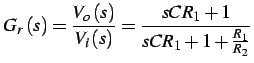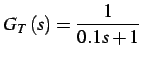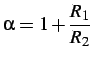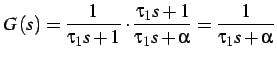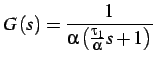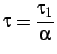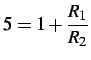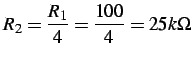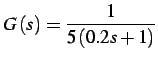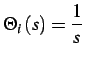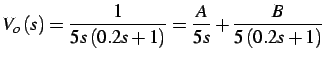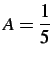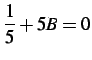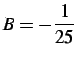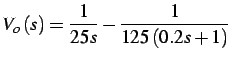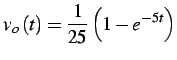Al fine di visualizzare l'andamento in funzione della frequenza della
funzione di trasferimento di un dato sistema, si utilizzano i diagrammi
di Bode. Questi permettono di visualizzare l'andamento della f.d.t.
in funzione della frequenza in 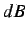 e la fase della stessa su appositi
diagrammi semilogaritmici. Sia:
e la fase della stessa su appositi
diagrammi semilogaritmici. Sia:
Example 5.5
Sia data una termocoppia
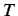
la quale ha, come funzione di trasferimento,
la grandezza:
con
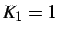
, il diagramma di Bode del sistema termocoppia è in
figura
![[*]](file:/usr/share/latex2html/icons/crossref.png)
.
Figure:
Diagramma di Bode del sistema termocoppia.
![\includegraphics[%
scale=0.5]{/home/angel/misure/misure44.eps}](img534.png)
|
Poiché la risposta non è adeguata all'utilizzo del dispositivo in
una catena di misura si decide di realizzare una rete, collegata tra
la termocoppia, ed il dispositivo di misura in grado di modificare
la risposta della termocoppia stessa.
Figure:
Termocoppia e rete di adattamento. 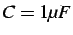 ,
,
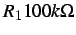 .
.
|
|
Il nuovo blocco inserito ha una funzione di trasferimento
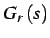
tale che il sistema ha funzione di trasferimento globale:
per valutare la funzione di trasferimento della rete
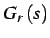
si valuta pertendo dalle equazioni circuitali della rete stessa. Se
si applica una tensione
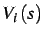
all'ingesso, lasciando
la rete a vuoto, si avrà una tensione d'uscita
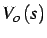
,
infatti:
ovvero:
la f.d.t. della rete anticipatrice è data da:
dove:
poichè deve essere
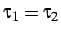
, si deduce che è:
mentre, ponendo:
ovvero:
il sistema ha una nuova costante di tempo data da:
volendo aumentare la risposta del nuovo sistema occore diminuire tale
costante di tempo, ad esempio si pone:
il che si traduce in:
da dove si calcola il valore della resistenza
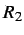
:
tale valore non è commerciale, per cui si pone:
il sistema ha fd.t.:
mentre per la risposta nel tempo a gradino unitario, si ha:
dove:
è il gradino unitario di variazione di temperatura:
dove le costanti
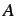
e
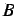
possono calcolarsi utilizzando il sistema
che si ricava dall'identità polinomiale:
cioè:
ed infine:
dalla quale antitrasformando:
Figure:
Risposte del sistema con la sola termocoppia
e con termocoppia + rete compensatrice.
![\includegraphics[%
scale=0.5]{/home/angel/misure/misure47.eps}](img572.png)
|
![]() e la fase della stessa su appositi
diagrammi semilogaritmici. Sia:
e la fase della stessa su appositi
diagrammi semilogaritmici. Sia:
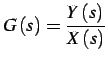
![$\displaystyle \Phi\left(s\right)=\arg\left[G\left(s\right)\right]=\arctan\frac{im\left[G\left(s\right)\right]}{re\left[G\left(s\right)\right]}$](img531.png)