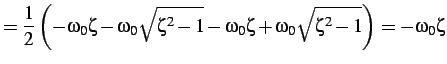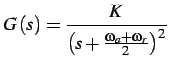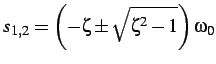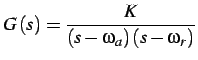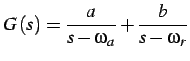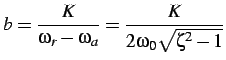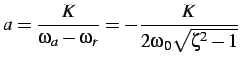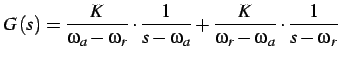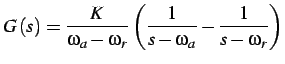Next: Risposta al gradino.
Up: Risposta in frequenza.
Previous: Risposta all'impulso.
Contents
Index
Per tali sistemi si ha:
ponendo come condizioni al contorno:
si ottiene:
e con le posizioni:
si ottiene:
la funzione di trasferimento del sistema è:
la precedente può assumere varie forme a seconda delle radici del
polinomio al denominatore, infatti risolvendo la seguente equazione:
cioè:
che si riduce allo studio di:
ponendo:
se
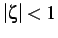 le soluzioni sono complesse e coniugate:
per
le soluzioni sono complesse e coniugate:
per
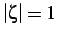 si hanno due soluzioni reali e coincidenti:
infatti:
ed infine per
si hanno due soluzioni reali e coincidenti:
infatti:
ed infine per
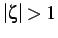 , si ha:
ovvero:
ovvero:
e di conseguenza:
, si ha:
ovvero:
ovvero:
e di conseguenza:
Figure:
Risposta in frequenza di un sistema del secondo ordine.
![\includegraphics[%
scale=0.5]{/home/angel/misure/misure49.eps}](img642.png)
|
Subsections





Next: Risposta al gradino.
Up: Risposta in frequenza.
Previous: Risposta all'impulso.
Contents
Index
Angelo Rossi
2003-12-05
![$\displaystyle a_{2}\left[s^{2}Y\left(s\right)-s\left.\frac{dy\left(t\right)}{dt...
...\left(s\right)-y\left(0\right)\right]+a_{0}Y\left(s\right)=b_{0}X\left(s\right)$](img611.png)
![$\displaystyle a_{2}\left[s^{2}Y\left(s\right)-s\left.\frac{dy\left(t\right)}{dt...
...\left(s\right)-y\left(0\right)\right]+a_{0}Y\left(s\right)=b_{0}X\left(s\right)$](img611.png)
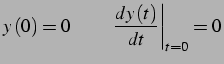
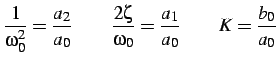
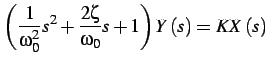
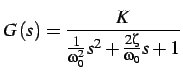
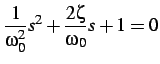
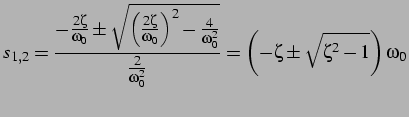
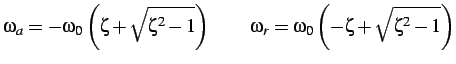
![$\displaystyle G\left(s\right)=\frac{K}{\left[s-\left(-\zeta-j\sqrt{\zeta^{2}-1}...
...ega_{0}\right]\left[s-\left(-\zeta+j\sqrt{\zeta^{2}-1}\right)\omega_{0}\right]}$](img623.png)
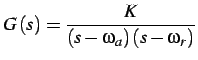
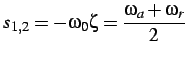
![$\displaystyle \frac{\omega_{a}+\omega_{r}}{2}=\frac{1}{2}\left[-\omega_{0}\left...
...rt{\zeta^{2}-1}\right)+\omega_{0}\left(-\zeta+\sqrt{\zeta^{2}-1}\right)\right]=$](img627.png)