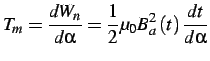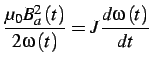- ...
speciali1.1
- Le unità di misura della temperatura accettate sono il Kelvin
 ed il grado centigrado Celsius
ed il grado centigrado Celsius 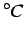 , essi sono dimensionalmente identici,
ma ci si riferisce ai primi senza specificare la parola ``gradi''.
La relazione tra i Kelvin e i gradi centigradi è la seguente:
dove
, essi sono dimensionalmente identici,
ma ci si riferisce ai primi senza specificare la parola ``gradi''.
La relazione tra i Kelvin e i gradi centigradi è la seguente:
dove
 è la temperatura in gradi centrigradi e
è la temperatura in gradi centrigradi e  quella in Kelvin.
quella in Kelvin.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... serie2.1
- In realtà può essere utilizzato lo stesso modello studiato per il
campione di resistenza.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... di2.2
- Sono coppie di elettroni che si muovono come fossero un tutt'uno.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
34.1
- E' un valore spesso applicato alla qualità e non all'affidabilità.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... canonica5.1
- gli ingressi canonici sono costituiti dal gradino, la rampa e l'impulso.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... potenziometrici6.1
- Per la misura di tensioni continue fino ad
 si possono usare
strumenti ad equipaggio mobile magnetoelettrici. Per tensioni più
elevate (maggiori di
si possono usare
strumenti ad equipaggio mobile magnetoelettrici. Per tensioni più
elevate (maggiori di  ) sono molto adatti i voltmetri elettrostatici.
Viceversa, per misurare tensioni molto basse e/o bassa temperatura
si adottano voltmetri superconduttori detti anche ad effetto Josephson
(v.). Qualche attenzione bisogna averla nel caso in cui la sorgente
di tensione provenga da un dispositivo ad alta impedenza (p.e. pila
Weston), per cui l'assorbimento di corrente dello strumento può influenzare
il valore della stessa tensione: la resistenza dello strumento do
misura deve essere molto più elevata della resistenza interna del
generatore. In questi casi si preferisce l'impiego di voltmetri magnetoelettrici
la cui resistenza può essere compresa tra i
) sono molto adatti i voltmetri elettrostatici.
Viceversa, per misurare tensioni molto basse e/o bassa temperatura
si adottano voltmetri superconduttori detti anche ad effetto Josephson
(v.). Qualche attenzione bisogna averla nel caso in cui la sorgente
di tensione provenga da un dispositivo ad alta impedenza (p.e. pila
Weston), per cui l'assorbimento di corrente dello strumento può influenzare
il valore della stessa tensione: la resistenza dello strumento do
misura deve essere molto più elevata della resistenza interna del
generatore. In questi casi si preferisce l'impiego di voltmetri magnetoelettrici
la cui resistenza può essere compresa tra i  ed i
ed i 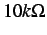 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elettrodinamometro6.2
- Questo è uno strumento elettrodinamico composto da due bobine: si
alimenta la bobina fissa con una corrente
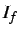 e l'altra, mobile
provvista di indice, con una corrente
e l'altra, mobile
provvista di indice, con una corrente 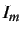 avente stessa frequenza
ma variabile in ampiezza e fase. La coppia media agente sulla bobina
mobile è:
dove
avente stessa frequenza
ma variabile in ampiezza e fase. La coppia media agente sulla bobina
mobile è:
dove 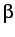 è lo sfasamento tra le due correnti. La coppia motrice
è nulla quando la corrente
è lo sfasamento tra le due correnti. La coppia motrice
è nulla quando la corrente 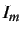 è nulla oppure quando
è nulla oppure quando 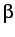 è pari a
è pari a
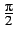 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ticonica7.1
- Dal nome di Tycho Brahe, fisico del XVI secolo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... curva7.2
- La coppia prodotta dalle due correnti è del tipo:
dove:
cioè la coppia
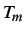 è la somma di due termini:
e:
è la somma di due termini:
e:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ha7.3
- L'energia immagazzinata dal campo nel disco di alluminio è:
se:
si ha:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.